
39 см, 44 см
Объяснение:
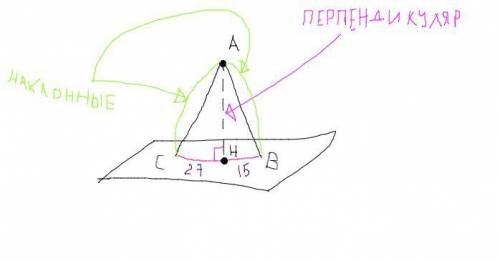
Прямые, проведенные из точки к плоскости, называются наклонными
Назовем данную точку A, опустим из нее перпендикуляр AH на плоскость.
Пусть B и C - точки пересечения прямых с плоскостью. Нужно найти AB и AC.
BH = 15 см, CH = 27 см
Большей наклонной соответствует большая проекция(есть такая теорема), поэтому AC > BC на 6 см.
Обозначим AB = x, тогда AC = x + 6
Треугольники AHB и CHB прямоугольные(потому что AH - перпендикуляр), поэтому для них действует теорема Пифагора:
AH^2 + BH^2 = AB^2
AH^2 + CH^2 = AC^2
Подставим в уравнения то, что известно: 27^2 = (30 - 3)^2 = 30^2+
AH^2 + 15^2 = x^2 3^2 - 2*30*3 = 909 - 180=
AH^2 + 27^2 = (x+6)^2 =729
Получается, AH^2 = x^2 - 15^2 = (x+6)^2 - 27^2
x^2 - 225 = x^2 + 12x + 36 - 729
12x = 729 - 225 - 36 = 504 - 36 = 468
x = 468 : 12 = 39
AB = x = 39 см
AC = x + 6 = 39 + 6 = 45 см
Теорема косинусов для треугольника AМC
AC^2=AM^2+MC^2-2*AM*CM*cosAMC
Теорема косинусов для треугольника BМC
BC^2=BM^2+MC^2-2*BM*CM*cosBMC
AC=BC (треугольник равносторонний) Тогда AC^2=BC^2
AM^2+MC^2-2*AM*CM*cosAMC=BM^2+MC^2-2*BM*CM*cosBMC
AM^2-2*AM*CM*cosAMC=BM^2-2*BM*CM*cosBMC
АМ и ВM знаем
22^2-2*22*CM*cosAMC=10^2-2*1010*CM*cosBMC
484-44*CM*cosAMC=100-20*CM*cosBMC
Углы ВМС и ВАС равны, опираются на одну дугу. ВАС=60 - равносторонний треугольник.
Угол АМС=АМВ+ВМС=АСВ+ВАС=60+60=120
484-44*CM*cos120=100-20*CM*cos60
484-44*CM*(-1/2)=100-20*CM*1/2
484+22*CM=100-10*CM
32*CM=-384
СМ=нет (отрицательное)