^2 - в квадрате, * - умножить
Здесь используется теорема синусов, которая гласит
стороны треугольника пропорциональны синусам противолежащих углов.
И теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
То есть
BC^2 = AB^2+AC^2-2*AC*AB*cos60
BC^2=6+4-2*2*(корень из 6)*0,5=10-2*(корень из 6)= приблизительно 5,1
BC = приблизительно 2,26
Это было по теореме косинусов
Теперь по теореме синусов
(корень из 6) / sinC = 2,26 / sin 60
sinC=sin60*(корень из 6) / 2,26
sinC=приблизительно 0,9
На калькуляторе есть специальная функция как искать угол по его синусу (2nd)
C = 64, 1580... = приблизительно 64,2, но можешь написать 64, 1
1)
Данный треугольник - равнобедренный, т.к. в нем второй угол тоже 45 градусов.
Треугольник, образованный средними линиями, будет подобен исходному,
т.к. катеты нового в точке пересечения с серединой гипотенузы образуют прямой угол, а сами катеты равны половинам исходных.
Коэффициент подобия равен 2 (средняя линия равна половине стороны, которой она параллельна).
Длину катетов равнобедренного прямоугольного треугольника найдем по формуле:
с²=2а², где с - гипотенуза, а - катеты
64=2а²
а²=32
а=4√2 см
Периметр большего треугольника равен
8+2*4√2=8(1+√2) см
Периметр треугольника, образованного средними линиями, относится к периметру исходного так же , как средние линии относятся к сторонам, которым они параллельны.
т.е 1:2
Периметр получившегося треугольника -
8(1+√2):2=4(1+√2) см
--------------------
2)
В треугольнике медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
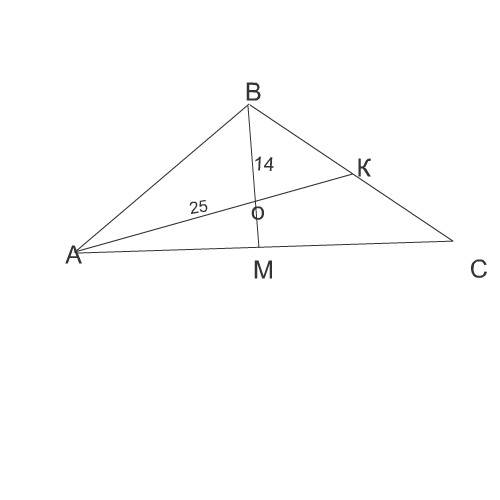
Смотрим рисунок.
Точка пересечения медиан отмечена О, пересечение медианы со стороной АС - М
со стороной ВС - К.
Дано:
АВС- равнобедренный треугольник.
ВО=14
АО=25
ОМ=ВО:2=7 см
Рассмотрим треугольник АОМ.
Он прямоугольный, т.к. в равнобедренном треугольника медиана=биссектриса=высота,если проведена к основанию.
По теореме Пифагора найдем АМ - половину АС.
АМ =√(25²-7²)=24
АС=24*2=48
ВМ=ВО:2*3=14:2*3=21
АВ=√(24²+21²)=≈31,89 см
АВ=ВС=≈31,89
x=12 cм