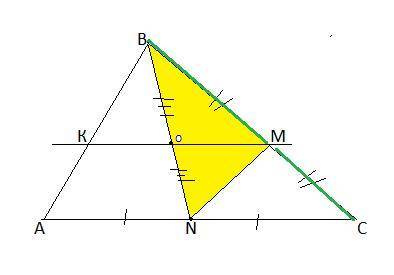
В треугольнике АВС проведена медиана ВN и средняя линия КМ. О-их точка пересечения. Какую часть площади треугольника АВС составляет площадь треугольника ОMN?
Объяснение:
Пусть S(ABC)=a
BN-медиана ⇒ S(ABN)=S(NBC) как имеющие равные основания и одинаковую высоту из точки В. S(ABN)=S(NBC)=1/2*а.
Т.к ВМ=МС ⇒ S(МВN)=S(МСN) как имеющие равные основания и одинаковую высоту из точки N . S(МВN)=S(МСN) =1/2*1/2*а=1/4*а.
KM║АС и М-середина ВС ⇒по т. Фалеса ВО=ОN .
Т.к ВО=ОN ⇒ S(ВМО)=S(ОМN) как имеющие равные основания и одинаковую высоту из точки М . S(ВМО)=S(ОМN) =1/2*1/4*а=1/8а.
Значит S(ABC) составляет 1/8 часть от S(ABC).
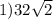 см²;
см²; 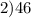 см².
см².
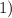 у многоугольника
у многоугольника 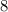 сторон и
сторон и 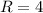 см.
см.
 данный многоугольник - восьмиугольный.
данный многоугольник - восьмиугольный.
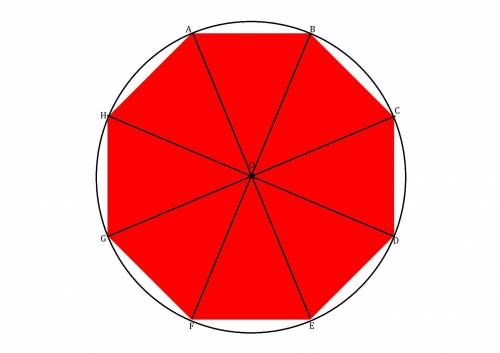
Обозначим данный восьмиугольник буквами 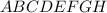 .
.
Около восьмиугольника 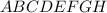 описана окружность с центром в точке
описана окружность с центром в точке 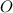 , по условию.
, по условию.
Проведём диагонали 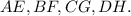 .
.
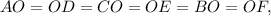 так как они радиусы описанной около шестиугольника окружности.
так как они радиусы описанной около шестиугольника окружности.
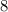 равных равнобедренных треугольников.
равных равнобедренных треугольников.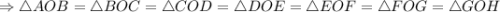 (а они ещё и равнобедренные).
(а они ещё и равнобедренные).

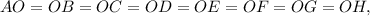 по свойству равнобедренного треугольника. Также эти стороны - радиусы описанной около данного восьмиугольника окружности.
по свойству равнобедренного треугольника. Также эти стороны - радиусы описанной около данного восьмиугольника окружности.
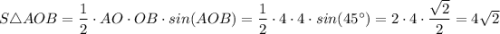 см²
см²
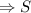 восьмиугольника =
восьмиугольника = 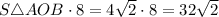 см².
см².
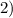 у многоугольника
у многоугольника 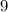 сторон и
сторон и 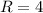 см.
см.
 данный многоугольник - девятиугольный.
данный многоугольник - девятиугольный.
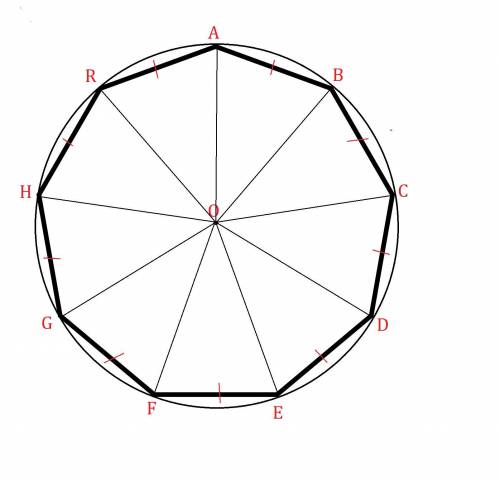
Обозначим данный девятиугольник буквами 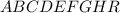 .
.
Около девятиугольника 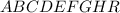 описана окружность с центром в точке
описана окружность с центром в точке 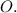
Соединим центр окружности с вершинами данного девятиугольника.
Отрезки 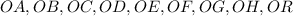 - радиусы описанной около девятиугольника окружности, поэтому они равны.
- радиусы описанной около девятиугольника окружности, поэтому они равны.
Итак, в данном девятиугольнике 9 равнобедренных равных треугольников:
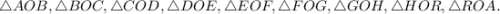
 см (они радиусы описанной окружности).
см (они радиусы описанной окружности).
В окружности всего 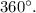
Тогда 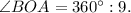
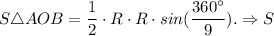 девятиугольника =
девятиугольника = 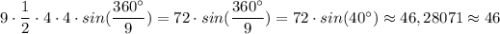 см²
см²
АВ=17;
АС вдвое больше, чем АВ;
ВС на 10 см меньше, чем АС;
Найти Р.
Решение.
Пусть АВ=х. Тогда АС=2х (по условию, АС вдвое больше, чем АВ), ВС=2х-10 (из условия).
Р=АВ+ВС+АС.
Р=х+2х+2х-10;
Р=5х-10;
Теперь подставим значение х= 17 см (из условия).
Р=5*17-10;
Р=85-10;
Р=75 (см).
ответ: периметр равен 75 см.