Объяснение:
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
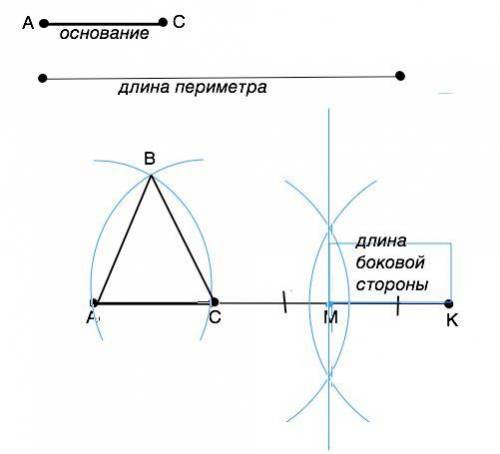
Объяснение:
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.

Відповідь:Для будь-якого трикутника АВС, існує точка О, рівновіддалена від усіх його вершин. Точка О - є центром описаного кола а відрізки ОА, ОВ, Ос-його радіусами. Якщо провести сединні перпендикулярно, то точка О буде належати серединному перпендикулярна, тобто точка О рівновіддалена від усіх вершин трикутника
Пояснення: