ответ: гипотенуза =20см
Объяснение: по свойствам угла 30°, катет лежащий напротив него равен половине гипотенузы. Меньший катет будет как раз он, потому что второй острый угол будет 60°, а наибольшая сторона лежит напротив большего угла и наоборот, поэтому катет, который лежит против угла 30° и будет наименьшим. Пусть тогда он будет "х", тогда гипотенуза будет 2х. Так как в сумме они составляют 30см, составляем уравнение:
х+2х=30
3х=30
х=30÷3
х=10; меньший катет=10. Теперь найдём гипотенузу: 2×10=20см.
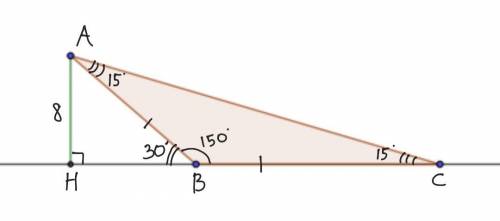
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
1. (x-1)²+(y+2)²=4, (x-1)²+(y+2)²=2²
уравнение окружности с центром в точке А(1;-2) и радиусом R=2
2. (x-1)²+y²=4, (x-1)²+(y-0)²=2²
уравнение окружности с центром в точке А(1;0) и радиусом R=2