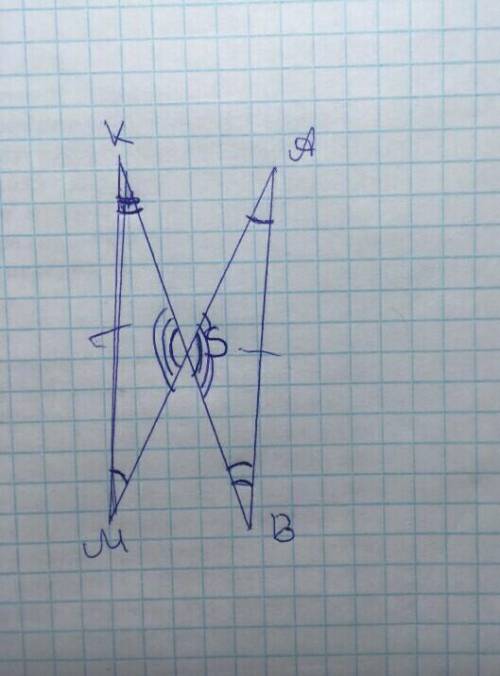
Дано:
KB ∩ AM = S.
AB = KM
AB || KM
Доказать:
S - середина KB и AM.
Решение.
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ 2 ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ.Рассмотрим △KSM и △BSA:
AB = KM
Т.к. AB || KM => ∠B = ∠K т.к. они накрест лежащие.В данном случае, действует теорема, которая написана заглавными буквами вверху, только обратная:
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ
∠A = ∠M, т.к. они накрест лежащие.
=> △KSM = △ASB, по 2 признаку равенства треугольников.
Т.к. △KSM = △ASB => S - середина KB и AM
Ч.Т.Д.
Объяснение:
Прежде чем находить эти треугольники, докажем, что ΔQOR - равнобедренный. Для равнобедренности треугольника достаточно, чтобы два угла в треугольнике были равны, что мы и видим по углам ∠OQR = ∠ORQ, значит он равнобедренный, и OQ = OR.
ΔERQ = ΔFQR по второму признаку: ∠EQF = ∠FRE, ∠ERQ = ∠FQR, QR - общая сторона
ΔEOQ = ΔOFR по второму признаку: ∠EQF = ∠FRE, ∠EOQ = ∠FOR (как вертикальные), OQ=OR (док-во расписано выше).
Больше равных пар треугольников нет.