Потому что если только вычесть из большего основание меньшее, то у нас получится сумма АЕ и МD, поэтому чтобы найти АЕ, мы ещё делим на два
1) ABCD - ромб , AB=BC=CD=AD=4 см , ВМ=2√3 см ,
∠АВС=150° ⇒ ∠BAD=180°-150°=30°
Проведём ВН⊥AD , ∠BHA=90° .
Из ΔАВН: ВН=АВ*sin30°=4*(1/2)=2 (см) .
МВ⊥ пл. АВСD ⇒ МВ⊥ любой прямой, лежащей в пл. ABCD ⇒
MB⊥BH ⇒ ΔАВН - прямоугольный , ∠МВН=90° ⇒ ΔМВН - прямоугольный.
Проведём отрезок МН, он будет наклонной, ВН - его проекция на плоскость АВСD , причём проекция ВН ⊥АD ⇒ по теореме о трёх перпендикулярах МН⊥AD , значит МН - расстояние от точки М до прямой AD.
МН найдём из прямоугольного ΔВНМ по теореме Пифагора:
МН=√(ВН²+ВМ²)=√(4+4*3)=√16=4 (см) .

(ты меня спрашивала в комментариях под вопросом)
Я учусь в 7-ом классе, но нашла в инете эту тему про дуги и связь её с углами. Оказывается, всё просто.
Назовём вписанный угол - ∠АСВ. Если у них с центральным углом АОВ общая дуга, на которую они опираются, то можно сделать вывод по свойству, которое я сейчас прочитала, что ∠АСВ в 2 раза меньше ∠АОВ. Там было написано, что центральный угол равен градусной мере дуги, на которую он опирается, а вписанный угол равен её половине. Поэтому, я сделала вывод, что:
60° - это и есть ∠АСВ, а угол АОВ => 60*2 = 120°.

Объяснение:
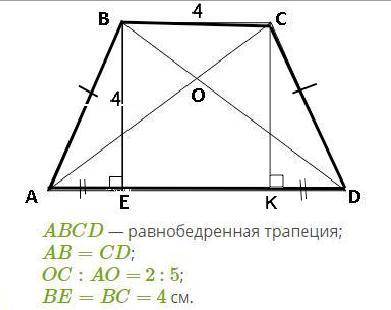
Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
В равнобедренной трапеции АВСD высота ВЕ делит AD на отрезки ЕD=(АD+BC):2 и AE=(AD-BC):2
Подробно:
Если опустить вторую высоту СК, получится прямоугольник ВСКЕ, в котором ЕК=ВС=4. Тогда треугольники АВЕ=КСD по гипотенузе и острому углу (в равнобедренной трапеции углы при основаниях равны). ⇒ АЕ=КD, поэтому каждый из этих отрезков равен половине разности между большим и меньшим основанием. Т.е. АЕ=КD=(AD-BC):2.
Так как в трапеции треугольники ВОС и АОD при основаниях подобны, все неизвестные элементы трапеции можно найти без труда.