ответ: 6 целых 4/7
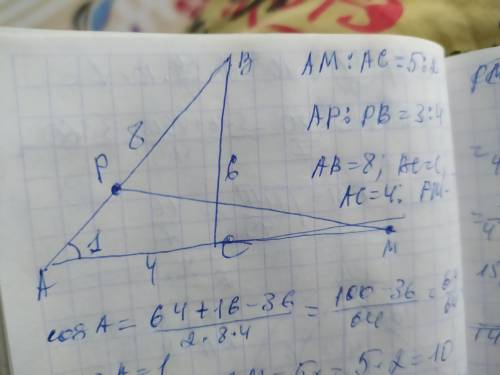
Объяснение: рассмотрим ∆АВС. В нём известны 3 стороны, и мы можем найти используя теорему косинусов угол А:
cosA=(AB²+AC²-BC²)/2×AB×AC=
=(8²+4²-6²)/2×8×4=(64+16-36)/64=64/64=1
cosA=1
Обозначим пропорции для разных сторон как: АМ=2х, 5х, а АВ как 3у, 4у
АМ=5х; АР=3х; ВР=4х
АС=4=2х.
2х=4
х=4÷2=2; х=2
АМ=5×2=10; АМ=10
Составим уравнение по стороне АВ:
3у+4у=8
7у=8
у=8/7
АР=3у=3×8/7=24/7;. АР=24/7
Найдём РМ, используя теорему косинусов: РМ²=АР²+АМ²-2×АР×АМ×cosA=
=(24/7)²+10²-2×24/7×1=
(576/49)+100-(480/7)= здесь находим общий знаменатель и получаем:
(576/49)+(4900/49)-(3360/49)=
=2116/49; РМ=√2116/49=46/7
или 6 целых 4/7
Дано :
Четырёхугольник ABCD - прямоугольник.
Отрезки АС и BD - диагонали.
АС ∩ BD = О.
CD = 15 см.
АС = 20 см.
Найти :
Р(ΔАОВ) = ?
Диагонали прямоугольника равны и точкой пересечения делятся пополам.На основе этих свойств, будет верна следующая запись -
АО = ОС = ВО = OD = АС/2 = 20 см/2 = 10 см.
Противоположные стороны прямоугольника равны.То есть -
CD = AB = 15 см.
Периметр - это сумма длин всех сторон.Отсюда -
Р(ΔАОВ) = АО + ОВ + АВ = 10 см + 10 см + 15 см = 35 см.
35 см.