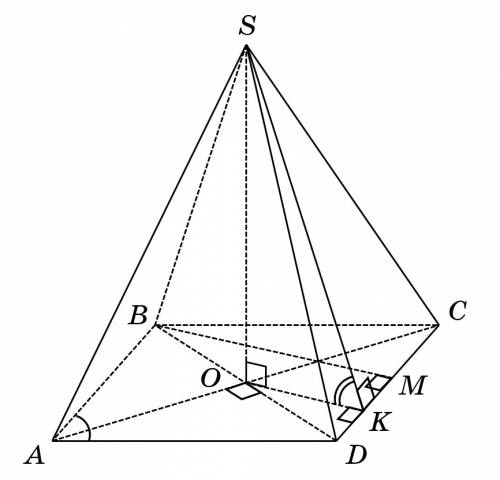
Пусть 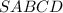 — четырёхугольная пирамида, в основании которой ромб
— четырёхугольная пирамида, в основании которой ромб 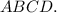 Меньшая диагональ ромба
Меньшая диагональ ромба 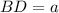 и острый угол
и острый угол 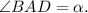
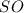 высота пирамиды, значит,
высота пирамиды, значит, 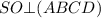 , следовательно
, следовательно 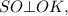 так как
так как 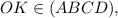
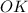 — проекция
— проекция 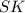 на плоскость
на плоскость 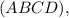
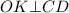 ⇒ по теореме о трёх перпендикуляров (ТТП)
⇒ по теореме о трёх перпендикуляров (ТТП) 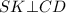 , следовательно,
, следовательно, 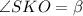 — линейный угол двугранного угла при ребре
— линейный угол двугранного угла при ребре 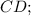 так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть
так как все двугранные углы при основании равны, то точка О — центр вписанной окружности, то есть 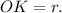
Найти: 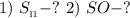
Решение. Ромб 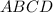 состоит из четырёх равных прямоугольных треугольников:
состоит из четырёх равных прямоугольных треугольников: 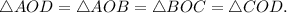
Рассмотрим 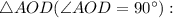
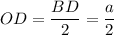
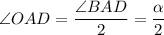
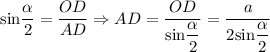
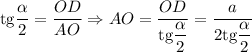
Значит, диагональ 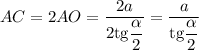
Рассмотрим 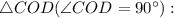
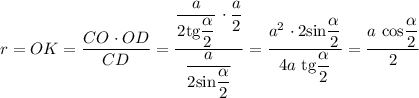
Высота ромба 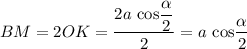
Площадь основания пирамиды 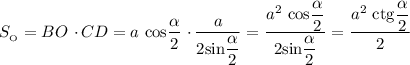
Рассмотрим 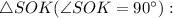
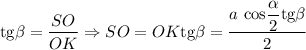
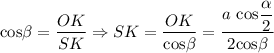
Определим площадь треугольника 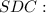
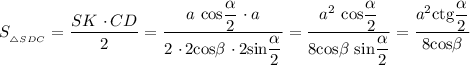
Из-за того, что у ромба все стороны равны и все двугранные углы при основании равны, то все боковые грани пирамиды будут тоже равны. Следовательно, площадь боковой поверхности 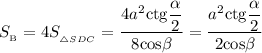
Теперь, зная площадь основания и боковой поверхности пирамиды можно найти площадь полной поверхности:
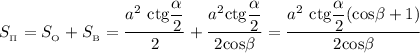
ответ: площадь полной поверхности пирамиды равна 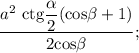 высота пирамиды равна
высота пирамиды равна 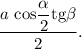
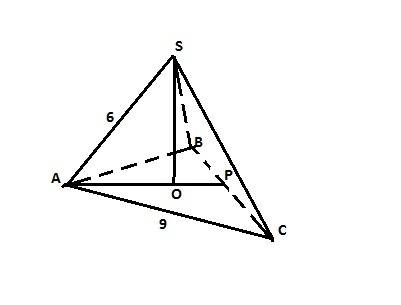
В правильной треугольной пирамиде вершина проецируется в центр основания - правильного треугольника. Этот центр делит высоту основания в отношении 2:1, считая от вершины треугольника. Высота треугольника равна (√3/2)*а, где а - сторона треугольника. В нашем случае h=(√3/2)*9. Тогда АО = (2/3)*h - это катет прямоугольного треугольника, образованного высотой пирамиды (второй катет) и ребром пирамиды (гипотенуза). АО=(√3*9/2)*(2/3) = 3√3. По Пифагору найдем высоту пирамиды: Н=√(SA²-(АО)²) или Н=√(36-27) = 3см. Это ответ.
Средняя линия треугольника - отрезок, соединяющий середины двух сторон. Средняя линия треугольника параллельна третьей стороне и равна половине этой стороны.
Пусть а, b, c -стороны треугольника. Среднии линии соответственно а/2, b/2, c/2.
а/2+b/2+c/2=11 см
Р=а+b+c=2*(а/2+b/2+c/2)
Р=2*11=22 (см)
ответ: периметр треугольника равен 22 см.