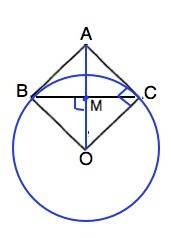
Отрезки касательных из одной точки до точки касания с окружностью равны. По свойству радиуса, проведенного в точку касания, ОВ⊥ВА; ОС⊥СА
∆ АВО=∆ АСО по 3-м сторонам ( по каким - укажите)
∆ ВАС - равнобедренный, ∠ ВАМ=∠САМ,
АМ биссектриса, высота, медиана ∆ ВАС и перпендикулярна ВС.
АМ=МО по условию, следовательно, ВМ - медиана прямоугольного треугольника, проведенная к гипотенузе, и
ВМ=АМ=ОМ (свойство), ⇒ ВС=АО
Четырехугольник, диагонали которого равны, взаимно перпендикулярны и при пересечении делятся пополам - квадрат.
⇒
∠ВАС=90°
2. |AB+AC|=|(12+12)√3=|24√3|=24√3
3. CD=√(0+4)²+(4+2)²=√16+36=√52