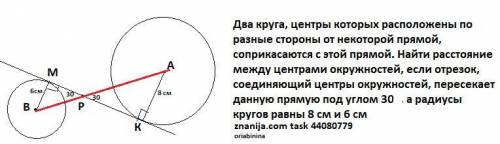
Два круга, центры которых расположены по разные стороны от некоторой прямой, соприкасаются с этой прямой. Найти расстояние между центрами окружностей, если отрезок, соединяющий центры окружностей, пересекает данную прямую под углом 30°, а радиусы кругов равны 8 см и 6 см
Объяснение:
Введем обозначения , как показано на чертеже. Расстояние между центрами это отрезок АВ. Он равен АР+ВР
1) ΔАКР-прямоугольный по свойству касательной и радиуса , проведенного в точку касания . Угол ∠АРК=30° , значит гипотенуза АР=2*8=16 (см).
2) ΔВМР-прямоугольный по свойству касательной и радиуса , проведенного в точку касания . Угол ∠ВРМ=30° , значит гипотенуза ВР=2*6=12 (см).
3) АВ=16+12=28(см) .
====================
Свойство " Радиус , проведенный в точку касания , перпендикулярен касательной.
Нарисуйте равнобедренный треугольник, постаравшись, чтобы угол против основания походил на угол в 30° (не обязательно).
Проведите из вершины угла при основании высоту к боковой стороне.
Получили наш любимый прямоугольный треугольник с острыми углами 30° и 60°. Высота исходного треугольника, как катет получившегося, который противолежит углу 30°, равна половине гипотенузы - боковой стороны.
Итак, имеем основание треугольника - боковую сторону - и высоту.
S=1/2 h·a
S=½ 3,5·7=24,5 :2= 12,25см²
