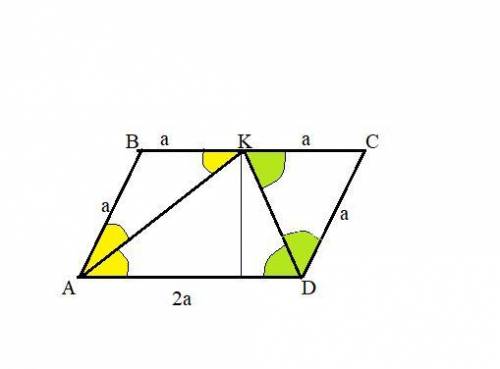
В параллелограмме ABCD биссектрисы углов A и D пересекаются в точке К,которая принадлежит стороне ВС.Найти площадь параллелограмма,если площадь треугольника AKD = 15 см^2.
Объяснение:
Пусть АВ=DС=а.
По свойству накрест лежащих углов при АD║BC и
-секущей АК ⇒∠DAK=∠AKB ⇒ΔABK равнобедренный и АВ=ВК=а ;
-секущей DК⇒∠АDK=∠СКD ⇒ΔDKС равнобедренный и DС =СК=а.
Значит AD=BC=2a
S(AKD)=0,5*AD*h=0,5*2а*h=a*h
S(ABK)+S(DCK)=0,5*ВК*h+0,5*КС*h=0,5h(BK+KC)=0,5h*2a=a*h ⇒
S(AKD)=S(ABK)+S(DCK)=15 (см²)
S( паралл)=S(AKD)+S(ABK)+S(DCK)=15+15=30 (см²)
Если A (0; 0) B (5; 0) C (12; -3) D (x, y). Точка D параллелограмма АВСД Найти координаты.
Объяснение:
Диагонали точкой пересечения делятся пополам . Найдем координаты точки О по формулам середины отрезка для АС :
х(О)= ( х(А)+х(С) )/2 у(О)= ( у(А)+у(С) )/2
х(О)= ( 0+12 )/2 у(О)= ( 0-3 )/2
х(О)= 6 у(О)= -1,5
О( 6 ;-1,5 )
В( 5 ;0) ,О( 6 ;-1,5). О-середина ВD ,найдем координаты т D
:
х(О)= ( х(В)+х(D) )/2 у(О)= ( у(В)+у(D) )/2
2*х(О)= х(В)+х(D) 2*у(О)= у(В)+у(D)
х(D) = 2*х(О)-х(В) у(D) = 2*у(О)-у(В)
х(D) = 2*6-5 у(D) = 2*(-1,5)+0
х(D) = 7 у(D) = -3
D(7 ; -3).