Если острый угол ромба 60 градусов ,то он своей малой диагональю разбивается на два равносторонних треугольника.Тогда его малая диагональ = 4 см.Диагонали ромба перпендикулярны и делятся в точке пересечения пополам.Рассмотрим прямоугольный треугольник АОВ, уголАОВ=90,АВ=4, ОВ=2 (как половина от малой диагонали ВД).По теореме Пифагора АО=square 12 (кв.корень из 12)=2*square3. Высота ОК этого треугольника, опущенная из точки О равна (АО*ОВ)/АВ (по свойству такой высоты),значит ОК=2*2*square3/4=square3. Так как стороны ромба равноудалены от точки М, то эта точка проектируется в центр окружности, вписанной в ромб.Радиусом этой окружности будет как раз высота ОК. Из прямоугольного треугольника МОК найдем ОМ.Длина перпендикуляра ОМ и есть расстояние от точки М до плоскости ромба. По теореме Пифагора ОМ=square(MK^2-OK^2)=square(25-3)=square22.
правильный шестиугольник имеет шесть равных сторон (обзовем а) и шесть равных внутренних углов
если соединить противолежащие вершины фигуры, то получим большие диагонали шестиугольника, которые являются также биссектрисами внутренних углов
центр вписанной окружности (обзовем т.О) совпадает с точкой пересечения больших диагоналей шестиугольника и делит диагонали пополам (отрезки b)
каждая сторона -а и два отрезка -b образуют ШЕСТЬ равных равнобедренных треугольников с вершинами в т.О (обзовем <A)
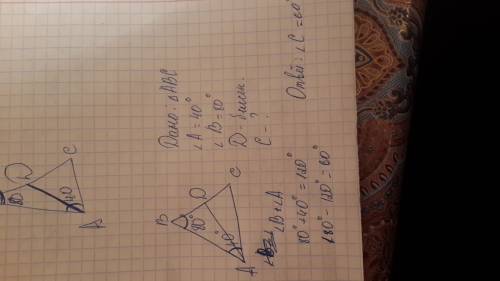
сумма всех ШЕСТИ углов с вершинами в т.О -образует полнный развернутый угол 360 град
значит один угол <A = 360 /6 =60 град
так как треугольники равнобедренные , то углы при основании (обзовем <B ; <C) равны
<B = <C = (180 - 60)/2 = 120/2 =60 град
так как все углы в треугольниках равны 60 град ,значит треугольники РАВНОСТОРОННИЕ , т.е. a = b
вписанная окружность касается каждой стороны шестиугольника, кратчайшее расстояние от центра окружности до точки касания - это перпендикуляр -это радиус окружности - это высота треугольника -r
высота треугольника (r), половина стороны шестиугольника (a/2) и отрезок (b)
образуют прямоугольный треугольник, тогда по теореме Пифагора
r^2 = b^2 - (a/2)^2 = a^2 - (a/2)^2 = a^2 (1-1/4) = a^2*3/4
тогда сторона шестиугольника a =r*2/√3
площадь каждого равностороннего треугольника S∆1 = 1/2*r*a =1/2*r*r*2/√3 =r^2/√3
площадь шестиугольника - это сумма ШЕСТИ треугольников
S = 6*S∆1 =6* r^2/√3 = 6*√3 r^2/ (√3*√3) = 6*√3 r^2/ 3 = 2√3 r^2
ДОКАЗАНО