(104+45√3)cм².
Объяснение:
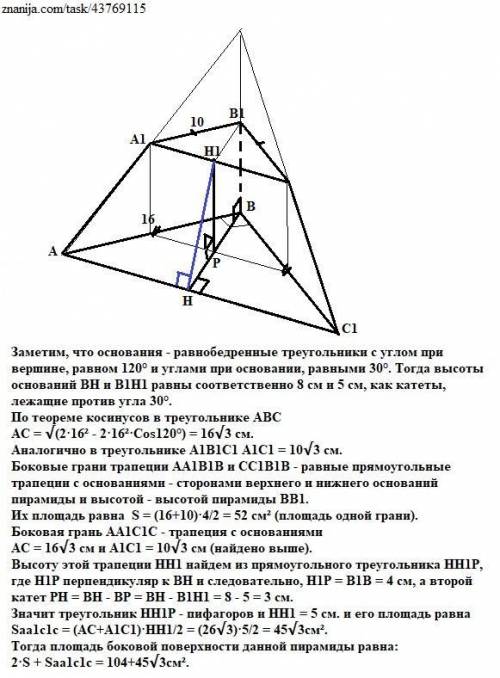
Заметим, что основания - равнобедренные треугольники с углом при вершине, равном 120° и углами при основании, равными 30°. Тогда высоты оснований ВН и В1Н1 равны соответственно 8 см и 5 см, как катеты, лежащие против угла 30°.
По теореме косинусов в треугольнике АВС
АС = √(2·16² - 2·16²·Cos120°) = 16√3 см.
Аналогично в треугольнике А1В1С1 А1С1 = 10√3 см.
Боковые грани трапеции АА1В1В и СС1В1В - равные прямоугольные трапеции с основаниями - сторонами верхнего и нижнего оснований пирамиды и высотой - высотой пирамиды ВВ1.
Их площадь равна S = (16+10)·4/2 = 52 cм² (площадь одной грани).
Боковая грань АА1С1С - трапеция с основаниями
АС = 16√3 см и А1С1 = 10√3 см (найдено выше).
Высоту этой трапеции НН1 найдем из прямоугольного треугольника НН1Р, где Н1Р перпендикуляр к ВН и следовательно, Н1Р = В1В = 4 см, а второй катет РН = ВН - ВР = ВН - В1Н1 = 8 - 5 = 3 см.
Значит треугольник НН1Р - пифагоров и НН1 = 5 см. и его площадь равна Saa1c1c = (АC+А1C1)·НН1/2 = (26√3)·5/2 = 45√3cм².
Тогда площадь боковой поверхности данной пирамиды равна:
2·S + Saa1c1c = 104+45√3cм².
1)
Центральный угол равен 94°, тоесть — противоположная ему дуга — равна 94°.
3)
На меньшую дугу AC — опирается угол <ABC, тоесть эта же дуга равна: <ACB*2 = 70*2 = 140°.
Дуга ACB — полуокружность, тоесть: меньшая ∪CB = 180-140 = 40°.
<A — опирается на меньшую дугу ∪CB, тоесть: <A = 40/2 = 20°.
<C = 180-(20+70) = 90°.
5)
Найти: <ACD; <AOD
Угол B — опирается на меньшую дугу AD, тоесть: ∪AD = <B*2 = 60*2 = 120°.
∪AD = 120° => <AOD = 120°.
<ACD — опирается на ту же меньшую дугу AD, тоесть: <ACD = ∪AD/2 = 60°.
1. S₁=a*b. a=5 см (H - высота прямого параллелепипеда), b=6 см (меньшая диагональ параллелепипеда)
S₁=5*6=30 (см²)
2. S₂=a*b. a=5 см, b=8 см
S₂=5*8=40 (см²)
2. S бок.пов.= P осн*H
Pосн=4*а (периметр ромба). а=?
прямоугольный треугольник:
катет а=3 см (1/2 меньшей диагонали ромба)
катет b= 4 см (1/2 большей диагонали ромба)
гипотенуза с - сторона ромба, найти оп теореме Пифагора:
c²=3²+4². c=5 см
или прямоугольный треугольник с катетами 3 и 4 - Пифагоров или Египетский треугольник, => гипотенуза =5
S бок. пов.= 4*5*5=100 (см²)
3. S полн.пов=S бок.пов.+2*Sосн
Sосн=(d₁*d₂)/2, Sосн=(6*8)/2=24 см²
Sполн.пов.=100+24=124 (см²)