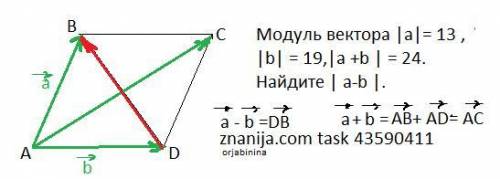
Модуль вектора |a|= 13 ,|b| = 19,|a +b | = 24. Найдите | a-b |.
Объяснение:
1) Рассмотрим ΔАВС, вектор а лежит на стороне АВ, вектор b лежит на стороне АD . Разность векторов а-b=DВ ( вектор) Уточняю длина ( или модуль) вектора равна длине отрезка на котором он лежит. Значит нужно найти отрезок DВ и АВ=13,АD=19 .
2) Достроим ΔАВD до параллелограмма , тогда сумма векторов а+b=АВ+АD=( по правилу параллелограмма ) = вектору АС. Тогда |AC|=|a+b|=24. Значит длина отрезка АС=24. По свойству диагоналей параллелограмма АО=12( О-точка пересечения диагоналей).
3) По свойству диагоналей параллелограмма: "сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон " имеем: AC²+BD²=2(AB²+AD²)
24²+BD²=2(13²+19²), BD=√(2*(169+361)-576)=√484=22.
В условии ошибка. Если сторона квадрата 24, то его диагональ 24√2 ≈ 34. Тогда в треугольнике ASC сторона АС больше суммы двух других сторон: 34 > 13 + 13, т.е. треугольник с такими сторонами не существует.
Встречается такая же задача с другими данными:
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Пирамида правильная, значит в основании лежит квадрат, а боковые грани - равные равнобедренные треугольники.
Проведем SH⊥CD. Тогда CH = HD (треугольник SCD равнобедренный).
CH = HD = 1/2 CD = 5.
ΔSCH: ∠SHC = 90°, по теореме Пифагора:
SH = √(SC² - CH²) = √(169 - 25) = √144 = 12
Sпов = Sосн + Sбок
Sосн = AD² = 10² = 100
Sбок = 1/2 Pосн · SH = 1/2 · 10 · 4 · 12 = 240
Sпов = 100 + 240 = 340 ед. кв.
d=10√2=14,14 см