Высота равнобедренного треугольника, проведенного к основанию 6, делит основание пополам. ( cм. рисунок в приложении) Высота разбивает равнобедренный треугольник на два прямоугольных с гипотенузой 5 см и катетом 3 см. Второй катет 4 см ( по теореме Пифагора, это египетский треугольник) S=6·4/2=12 кв. ед Вершина пирамиды проектируется в центр описанной окружности (см. рисунок, три прямоугольных треугольника равны по катету ( высота пирамиды - общая и острому углу) r=S/p=12/(5+5+6)/2=24/16=3/2=1,5 H=r·tg60°=1,5·√3=3√3/2
Даны координаты вершин треугольника ABC
А(-4;10), В(8;1) , С(12;23) . Найти: 1) уравнение высоты CD и ее длину ;
2) уравнение медианы AE и координаты точки К , точки пересечения этой медианы с высотой CD.
Объяснение:
1) Прямые содержащие отрезки АВ и СD будут перпендикулярны , те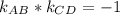
Уравнение прямой АВ :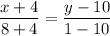 или 12(у-10)=-9(х+4) ,
или 12(у-10)=-9(х+4) ,
4(у-10)=-3(х+4) , у-10= -0,75(х+4) , у= -0,75х+7.
Для уравнение прямой СD , у=4/3*х+b , найдем в используя координаты С(12;23).
CD=√( (12-х₂)²+(23-у₂)² ), где C(12;23), D(х₂;у₂ )
Ищем координаты D
СD=√( (12-0)²+(23-7)² )=√(144+256)=20.
2)Если АЕ-медиана , то Е середина ВС .
Е( (8+12):2 ; (1+23):2 ) или Е(10;12)
Уравнение прямой АЕ :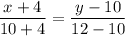 или 14(у-10)=2(х+4) ,
или 14(у-10)=2(х+4) ,
у-10=1/7*(х+4) , у-10= 1/7*х+4/7 , у=1/7*х+74/7.
Ищем координаты точки К
25x=75 , x=3 . Тогда у= 1/7*(3+74)==11 ⇒ К(3;11).