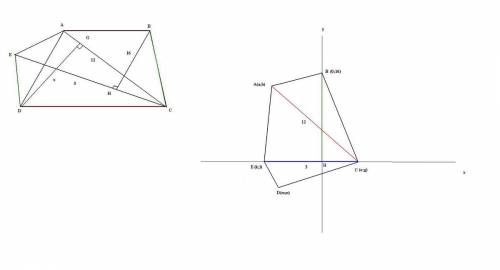
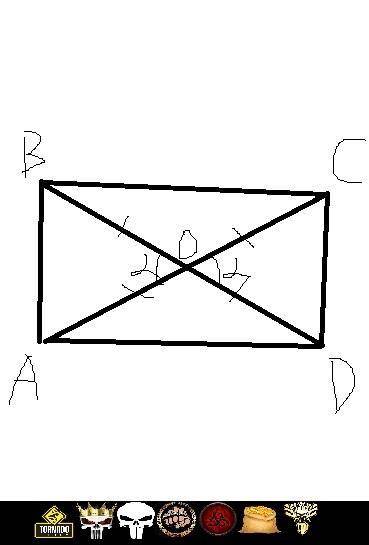
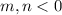Колодцы в которых вода поднимается на поверхность под большим напором в казахистане называюи

👇

Увидеть ответ

Ответ:

Hgfdc

12.07.2022

Колодцы, вода в которых поднимается под давлением на поверхность, названы вчесть провинции Артуа- во Франции

4,8(1 оценок)

Открыть все ответы

Ответ:

макарена2

12.07.2022

Начертим равные отрезки BD и AC. Пусть точка их пересечения - О.

По условию, О делит оба отрезка пополам. А так как BD=AC, то

BO=OC=OA=OD

Начертим так же стороны четырехугольника ABCD.

Надо доказать, что это прямоугольник. BD и AC - его диагонали, они же пересекающиеся прямые. Тогда пусть ∠BOA=α, ∠BOA=∠COD=α (вертикальные). ∠BOA и ∠BOC - смежные ⇒ ∠BOA + ∠BOC = 180° ⇒ ∠BOC=180°-∠BOA=180°-α

Отметим также, что ΔBOA=ΔCOD (по 2 сторонам BO=OD, CO=OA, и углу между ними ∠BOA=∠COD). Аналогично ΔBOC=ΔDOA (BO=OD, CO=OA, ∠BOC=∠DOA).

Из этого следует (второе доказанное равенство треугольников), что ∠OBC=∠ODA, а это накрест лежащие углы при пересечении прямых BC и AD секущей BD, то есть BC║AD.

∠OBA=∠ODC (из первого доказанного равенства треугольников), а это накрест лежащие углы при пересечении прямых AB и CD секущей AC, то есть AB║CD.

Из равенств треугольников следует, что BC=AD (2-ое равенство), а AB=CD (1-ое равенство). В четырехугольнике ABCD противолежащие стороны равны и параллельны, то есть это параллелограмм. Осталось доказать, что хотя бы один угол в нем прямой (тогда найдется ещё один противополежащий равный ему угол, останутся два равных между собой угла, а так как их сумма 180° (сумма углов четырехугольника 360 и минус 2 угла по 90°), то они тоже будут по 90°).

Рассмотрим ∠ABC:

∠ABC=∠ABO+∠OBC;

из ΔOBA, который равнобедренный, углы при основании равны ∠ABO=∠BAO = (180°-α)/2=90°-α/2

из ΔOBC, который равнобедренный, углы при основании равны

∠OBC=∠OCB=(180°-(180°-α))/2=α/2

∠ABC=∠ABO+∠OBC=90°-α/2+α/2=90°, то есть в параллелограмме ABCD все 4 угла прямые, значит, это прямоугольник. Что и требовалось доказать.

Докажите,что если два равных отрезка пересекаются в их общей середине, то их концы являются вершинам

4,8(41 оценок)

Ответ:

cat73309owz9do

12.07.2022

Предложу аналитическое решение
Впишем наш пятиугольник в систему координат OXY

, так чтобы $BH|| OY\\
EC|| OX$ , где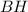

есть расстояние,тогда очевидно координата B(0;16)

,тогда $E(k;0)\\
C(e;0)$ где e;k

координаты абсцисс соответствующих точек.
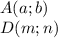Обозначим так же координаты $A(a;b)\\ D(m;n)$ , и условимся что
m;n

, так как иначе пятиугольник будет не выпуклый, что следует из анализа самой задачи.
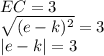
Так как $EC=3\\
\sqrt{(e-k)^2}=3\\
|e-k|=3\\
$
положим что $e=1\\
k=-2\\
$ что верно по условию , так как

. То есть сама задача сводится на нахождение такой конструкций пятиугольника, что все компоненты будут верны, иными словами параллельность и длины.
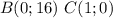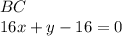Так как мы знаем координаты точек $B(0;16) \ C(1;0)$ , то его уравнение $BC\\
16x+y-16=0$ по известной формуле по двум точкам.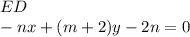
уравнение $ED\\
-nx+(m+2)y-2n=0$
а так как они параллельны , то выполняется условие
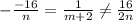
$-\frac{-16}{n}=\frac{1}{m+2} \neq \frac{16}{2n}$
Вторую часть
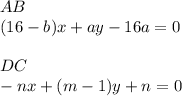
$AB\\ 
 (16-b)x+ay-16a=0\\\\
 DC\\ 
 -nx+(m-1)y+n=0$
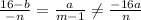
так же $\frac{16-b}{-n}=\frac{a}{m-1} \neq \frac{-16a}{n}$
И выполняется условие
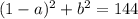(1-a)^2+b^2=144

то есть это длина отрезка

.

из уравнения
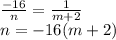
$\frac{-16}{n}=\frac{1}{m+2}\\
 n=-16(m+2)$
так как n-2

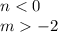, возьмем

, тогда

, что верно по условию m,n

Откуда получается система для второй точек координат
$-32+2b=16a\\ 
 (1-a)^2+b^2=144$
из решения получаем
$a=\frac{12\sqrt{61}-127}{65}\\
b=\frac{24(4\sqrt{61}+1)}{65}$

и все условию будут выполнены
Теперь по формуле нахождения расстояние от точки до прямой
уравнение

$AC\\
 2*(4+\sqrt{61})+3y-2(4+\sqrt{61})=0$
координата точки D(-1;-16)

откуда расстояние равно
$\frac{|-1*2(4+\sqrt{61})-3*16 - 2(4+\sqrt{61})|}{\sqrt{(2(4+\sqrt{61}))^2+3^2}}=4$

Впятиугольнике,ав║cд, дe║bc ас=12,ес=3,от в до ес = 16,от д до ас?