1.
Расстояние между точкой A & прямой a — проекция наклонной Ba, или просто — катет.
Другого определения здесь невозможно дать, этот треугольник обязательно должен быть прямоугольным.
<B = 30°; Теоерема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Напротив угла <B — лежит катет Aa, тоесть: Aa = Ba/2.
Катет Aa — мы можем найти только теоремой Пифагора:
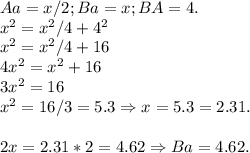
Вывод: Aa = 2.31.
2.
<A = 90°; <B == <C => BA == AC.
BC (гипотенуза) = 14; по теореме Пифагора:
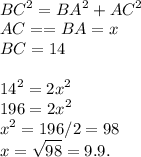
Нарисуем дополнительную высоту, проведённую через прямой угол: Высота AM.
В равнобедренном прямоугольном треугольнике — высота, проведённая к гипотенузе — это — и медиана, и высота, и биссектриса.
То есть: AM == MC = 14/2 (свойство медианы в прямоугольном треугольнике) = 7.
Вывод: AM = 7.
3.
<B = 30° => AC = BC/2 (теорема о 30-градусном угле).
Опять же, теорема Пифагора:
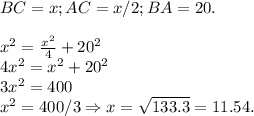
Высоту нарисуем дополнительную, в рисунке — её нет.
Добавим новую точку на гипотенузе BC — пусть будет — M.
Отрезок AM — это и есть расстояние между прямой a — и точкой A.
<MAC = 90 - <C = 90-60 = 30° => MC = AC/2 (теорема о 30-градусном угле).
MC = AC/2 => MC = 11.54/2 = 5.8.
По теореме Пифагора:
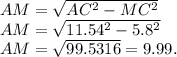
Вывод: MC = 9.99.
\\ВНИМАНИЕ!
Теорема Пифагора такова: Сумма квадратов катетов равна квадрату гипотенузы, тоесть: 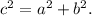 \\
\\
Ниже
Объяснение:
1.У равнобедр. треугольника углы при основании равны, так что угол А равен С и они оба равны углу КМС. АС в данном случае секущая, у которой углы А и КМС равны, а раз они равны, то прямые АВ и МК параллельны
2. равны, 32 градуса
3. Угол 1 и 3 равны по как соответственные при параллельных прямых, то-есть каждый из них по 130 градусов. Сумма односторонних углов равна 180 градусам, то-есть угол 2 = 180-130=50 градусов.
4. х+36, х+x+36=180, x=(180-36)/2, 72, 36. Через запятую стоит то, что должно быть в полях если что.
5. 7х+8х=180, тогда 15х =180, а х=180/15=12. Тогда первый угол, который равен 7х будет 7*12=84, а второй будет 8*12=96.
у-1=к(ч-1)
кх-у+(1-к)
Нормирующий множитель
N=+-1/√(1+k²)
После приведения уравнения к нормальному виду оно запишется в виде:(kx-y+(1-k))/(+-√(1+k³)
Pасстояние между точкой и прямой определяется по формуле
d=|(Ax1+By1+C)/√(A²+B²)|
2=|(-k-2+1-k)/√(1+k²)|
2√(1+k²)=|-2k-1|
4(1+k²)=4k²+4k+1
4k²+4k-4k²=4-1
4k=3
k=3/4
Подставим в уравнение
y-2=3/4*(x+1)
y=3/4*x+3/4+2=3/4*x+11/4