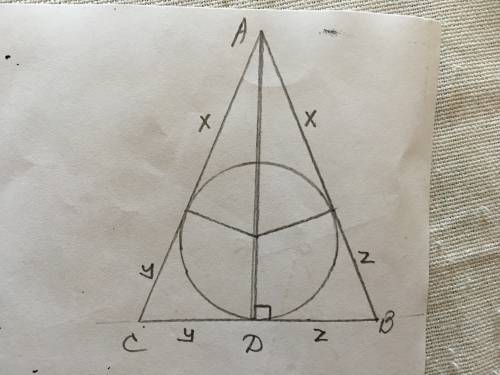
Первый случай, все три прямые могут совпасть в одну не годится т.к. по условию есть пересекающиеся.
Второй случай, две прямые совпали, а третья их пересекает в одной точке, тогда 4 части.
Третий случай, все три прямые пересекаются в одной точке, тогда 6 частей.
Четвёртый случай, каждая прямая пересекает другие две в различных точках, тогда 7 частей.
Пятый случай, две прямые параллельные, а третья пересекает каждую из параллельных, тогда 6 частей.
Шестой случай, две прямые параллельные, а третья совпадает с одной из них не годится т.к. по условию есть пересекающиеся.
Седьмой случай когда все три прямые параллельны не годится т.к. по условию есть пересекающиеся.
ответ: на 4, 6 или 7 частей.
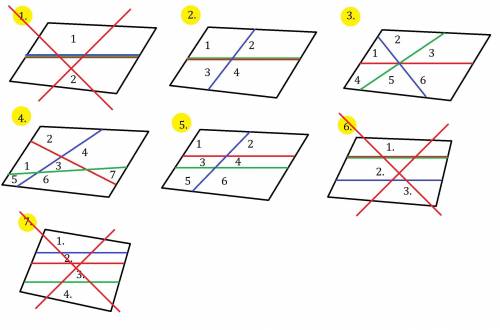
Пусть одна часть равна х.
ВС=2 1/7х; АС=2 6/7х. АВ=2 1/7 + 2 6/7=5.
По теореме Пифагора АВ²=ВС²+АС²,
25=(2 1/7х)²+(2 6/7х)²,
25=225/49 х²+400/49х²,
625х²/49=25,
х²=25·49/625=49/25,
х=√49/25=7/5=1 2/5=1,4.
АВ=2 1/7 ·1,4=3 л ед.
АС=2 6/7 ·7/5=20/7 ·7/5=4 л. ед.
ответ: 3 л. ед., 4 л.ед.