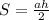Основания прямоугольной трапеции равны 15 дм и 19 дм. меньшая боковая сторона равна 3 дм. вычисли большую боковую сторону трапеции.

👇

Ответ:

Nastya165567

03.06.2023

По этому рисунку мынаходим HD.
HD=AD-AH
AH=BC=15(т.к противоположн. стороны в прямоугольнике равны)
hd=19-15=4
ch=ab=3
cd²=ch²+hd²=3²+4²=9+16=25
cd=√25=5
ответ: CD=25 дм.
Основания прямоугольной трапеции равны 15 дм и 19 дм. меньшая боковая сторона равна 3 дм. вычисли бо

Основания прямоугольной трапеции равны 15 дм и 19 дм. меньшая боковая сторона равна 3 дм. вычисли бо

4,6(73 оценок)

Открыть все ответы

Ответ:

ekaterinahbjdnxКатя

03.06.2023

В данном треугольнике каждая сторона больше 4, что можно доказать теоремой Пифагора (если рассматривать прямоугольные треугольники, где сторона начерченного является гипотенузой. Один из катетов везде больше или равен 4, другой - больше или равен 1, значит, гипотенуза больше большего, скажем так).

Разберёмся с площадью.
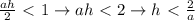
Площадь треугольника находится по формуле $S= \frac{ah}{2}$ , отсюда: $\frac{ah}{2} \ \textless \ 1 \rightarrow ah\ \textless \ 2 \rightarrow h\ \textless \ \frac{2}{a}$
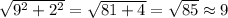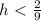
Пусть h - высота, проведённая к большей стороне, a - большая сторона. По теореме Пифагора она равна $\sqrt{9^2+2^2}= \sqrt{81+4}= \sqrt{85}\approx9$ . Тогда $h\ \textless \ \frac{2}{9}$
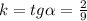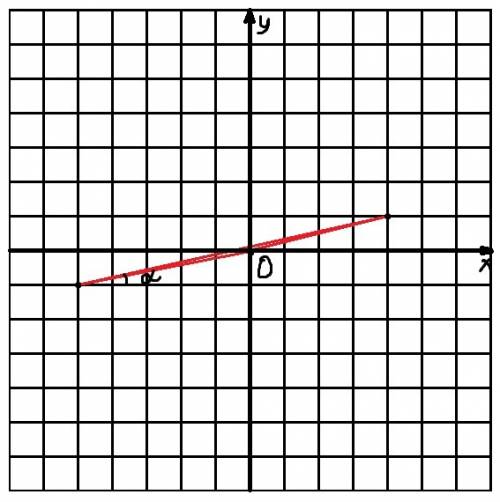
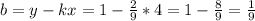Рассмотрим треугольник в системе координат с точкой, лежащей против большей стороны, в начале координат. Найдём уравнение прямой, на которой лежит большая сторона (y=kx+b). $k=tg\alpha= \frac{2}{9}$ , $b=y-kx=1- \frac{2}{9} * 4=1- \frac{8}{9} = \frac{1}{9}$ . Теперь рассмотрим прямоугольный треугольник из высоты и стороны на Oy, равной b. Действительно, если точка лежит на оси Oy, то её координата по x = 0, а значит, её координата y = k * 0 + b = b. В данном случае сторона на Oy будет гипотенузой, а высота - катетом. Следовательно, она меньше гипотенузы. Т. е. 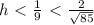$h\ \textless \ \frac{1}{9} \ \textless \ \frac{2}{\sqrt{85}} }$ (доказательство того, что 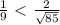$\frac{1}{9} \ \textless \ \frac{2}{ \sqrt{85} }$ , могу провести в комментариях, если потребуется), значит, 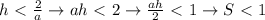$h\ \textless \ \frac{2}{a} \rightarrow ah\ \textless \ 2\rightarrow \frac{ah}{2} \ \textless \ 1\rightarrow S\ \textless \ 1$ . Начерченный треугольник удовлетворяет всем условиям.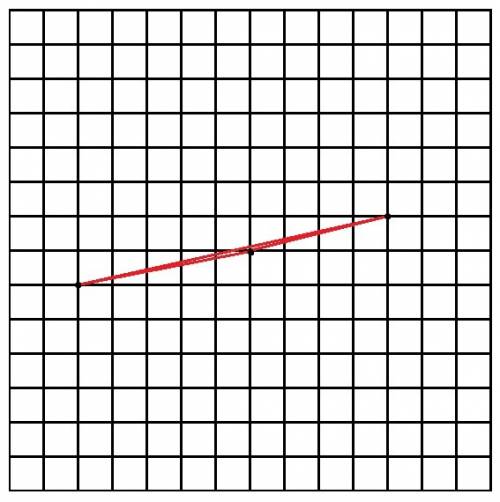
Нарисуйте треугольник с вершинами в узлах квадратной сетки со стороной 1, у которого все стороны дли

Нарисуйте треугольник с вершинами в узлах квадратной сетки со стороной 1, у которого все стороны дли

4,6(89 оценок)

Ответ:

rasimallamurato

03.06.2023

Пусть даны стороны длиной:
АВ = 2 см, ВС = 3 см, СД = 4 см и АД = 5 см.
Дан угол в 40 градусов между сторонами АД и ВС.

Откладываем горизонтальный отрезок длиной 5 см - это сторона АД.
Из концов АД в точках А и Д проводим окружности радиусом, равным длинам АВ и СД, то есть радиусами 2 и 4 см.
Из точки на продолжении стороны АД проводим луч под углом 40 градусов к прямой АД.
Затем с треугольника и линейки делаем параллельный перенос этого луча так, чтобы длина отрезка между точками на окружностях равнялась длине стороны ВС, то есть 3 см.
После соединения найденных точек с А и Д получаем заданный четырёхугольник АВСД.
Построить четырёхугольник, зная четыре его стороны и угол между двумя противоположными сторонами