Тут, наверное, площадь поверхности шара, которая равна 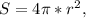 где r - радиус шара. Остается только найти r. Пусть сторона куба равна а. Тогда
где r - радиус шара. Остается только найти r. Пусть сторона куба равна а. Тогда 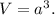 По условию задачи V=125. Тогда
По условию задачи V=125. Тогда 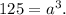 Тогда а=5. Теперь можно рассмотреть сечение куба, где у шара будет свой диаметр. В сечении получаем квадрат со стороной 5, внутрь которого вписана окружность. Очевидно, что диаметр этой окружности совпадает с длиной стороны квадрата, то есть d=5. d=2r, 2r=5, r=2,5. Подставим в вышеуказанную формулу.
Тогда а=5. Теперь можно рассмотреть сечение куба, где у шара будет свой диаметр. В сечении получаем квадрат со стороной 5, внутрь которого вписана окружность. Очевидно, что диаметр этой окружности совпадает с длиной стороны квадрата, то есть d=5. d=2r, 2r=5, r=2,5. Подставим в вышеуказанную формулу.
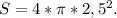
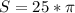
Если хотите приближенно.
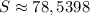
Решение.
Согласно теореме косинусов
a2=b2+c2 - 2bc*cosальфа
Откуда
AC2 = AB2 + BC2 - 2*AB*BC*cos 120
AC2 = 25 + 9 - 2*5*3*cos 120
Косинус 120 градусов найдем по таблице значений тригонометрических функций.
AC2 = 34 - 30 (-0.5)
AC2 = 49
AC = 7
Каждая из граней боковой поверхности представляет собой прямоугольник. При чем длина одной из сторон прямоугольников одинакова и равна высоте призмы. Таким образом, боковая грань призны наибольшей площади лежит на той стороне основания, длина стороны которого наибольшая.
То есть наибольшая из боковых граней имеет длину основания 7 см.
Откуда высота призмы равна 35 / 7 = 5 см
Таким образом, площадь боковой поверхности будет равна сумме площадей каждой из боковых граней
S = 5*5 + 3*5 + 7*5 = 75 см2
ответ: 75 см2 .