ответ: 54
Объяснение: 1) S трапеции =1/2*h*(BC+AD)
=>S трапеции ABCD=1/2*h*(6+12)=1/2*h*18=9*h
2) Проведем высоту из вершины С. Тогда трапеция поделится на прямоугольник ABCH(т.к все углы =90 градусов) и треугольник CHD. Рассмотрим треугольник CHD. В нем:
угол CDH=45
угол CHD=90
=> угол HCD=45(тк сумма углов в треугольнике =180 градусов)
Тк два угла равны, то треугольник равнобедренный (по признаку равнобедренного треугольника)=>HD=CH
Тк BCHD - прямоугольник, то BC=AH=6(по свойству параллелограмма (а любой прямоугольник - это параллелограмм)
HD=AD-AH=12-6=6
=>CH=HD=6
Значит, высота трапеции = 6
Значит, S трапеции ABCD=9*6=54 см
Старалась максимально подробно, рисунок в прикрепленном файле
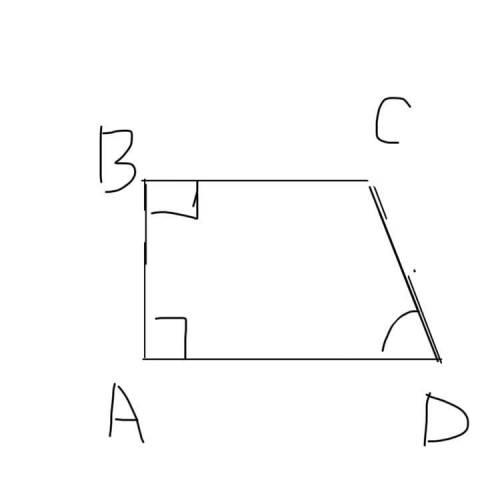
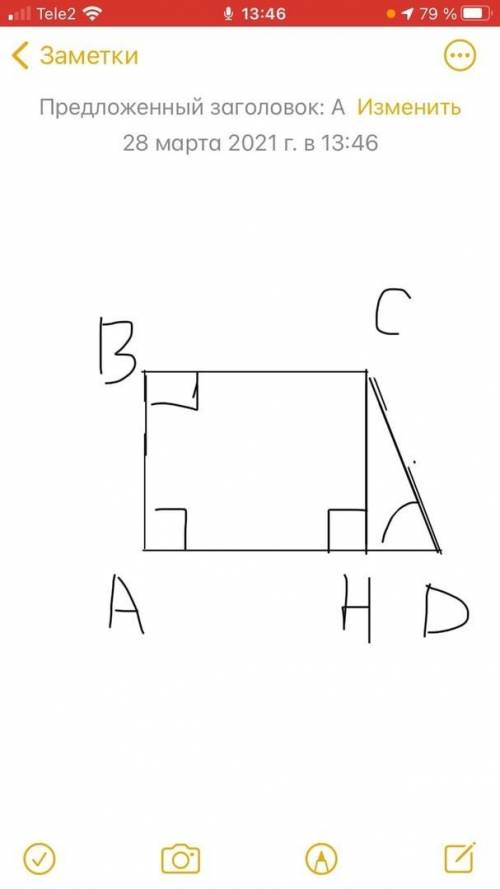
О - пересечение АВ и CD
АО=ОВ
СО=ОD
Доказать: АС || ВD
Док-во:
Рассмотрим треугольники АОС и ВОD. Они равны по первому признаку равенства треугольников: АО=ОВ и СО=ОD (по условию), угол АОС= углу ВОD (как вертикальные).
Из равенства треугольников следует, что угол САО= углу ОВD, а угол АСО=углу ОDВ. Так как внутренние накрест лежащие углы САО и ОВД, образованные прямыми АС и ВD и секущей АВ, равны, то прямые АС и ВD параллельны, ч.т.д..
Аналогично, так как внутренние накрест лежащие углы АСО и ОDВ, образованные прямыми АС и ВD и секущей СD, равны, то прямые АС и ВD параллельны, ч.т.д..