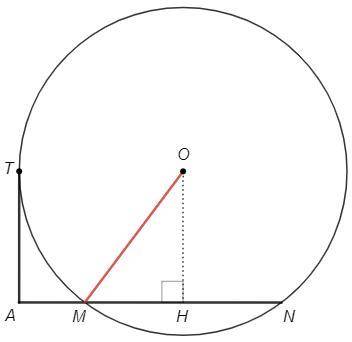
Из точки А, не лежащей на окружности, проведены к окружности касательная и секущая. Расстояние от А до точки касания 12 см. Расстояние от A до одной из точек пересечения секущей с окружностью 24 см. Найдите радиус окружности, если секущая удалена от центра на 12 см.
В сантиметрах
По теореме о касательной и секущей
AT^2 =AN*AM => 12^2 =24*AM => AM =144/24 =6
MN =AN-AM =24-6 =18
Расстояние от точки до прямой - длина перпендикуляра.
OH⊥AN, OH=12
Перпендикуляр из центра к хорде делит ее пополам.
MH =MN/2 =9
По теореме Пифагора
OM =√(OH^2 +MH^2) =15 (см)
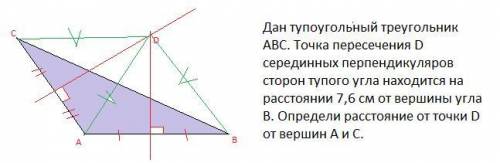
Дан тупоугольный треугольник ABC. Точка пересечения D серединных перпендикуляров сторон тупого угла находится на расстоянии 7,6 см от вершины угла B. Определи расстояние от точки D от вершин A и C.
Объяснение:
Точка D лежит на серединном перпендикуляре к отрезку АВ → равноудалена от концов отрезка АВ → DB=7,6 см, значит DA=7,6 см.Точка D лежит на серединном перпендикуляре к отрезку АС → равноудалена от концов отрезка АС→ DА=7,6 см, значит DС=7,6 см.===========================
Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
пусть радиус окр.=а, тогда сторона квадр.=2*а
в правильном Δ высоты пересекаются и делятся т. пересечения в соотношении 2:1, тогда в Δ полученном из радиусов и основанием вписанного треугольника высота =а/2
сторона вписанного треугольника=2*√(а²-(а/2)²)=2*√(а²*3/4)=а*√3
Δ/квадр=а*√3/(2*а)=√3/2