1.Дано: АВСД - трапеция, ВС//АД,ВС=20см, АД=60см, АВ=13см, СД=37см.
Найти: S
Из точек В и С опустим перпендикуляры на сторону АД. Совместим эти линии - получим треугольник со сторонами 13,37 и 40 (60-20=40).
По формуле Герона площадь этого треугольника равна:
√[45(45-13)(45-37)(45-40)]=√(45*32*8*5)=240 кв.см
а его высота:
240*2:40=120 см (использ.формулу S=1/2 a*h).
Sтрапеции=1/2(ВС+АД)*h=(20+60)*120:2=480 кв.см
2.Дано: АВСД - трапеция, ВС//АД, АД=44см, АВ=СД=17см, АС=39см.
Найти: S
По формуле Герона Площадь треугольника АСД равна:
√[50(50-39)(50-17)(50-44)]=330 кв.см
а его высота СМ:
330*2:44=15 см
По теореме Пифагора:
МД=√(СД^2-СМ^2)=289-225=8 см
ВС=АД-2МД=44-16=28 см
Sтрапеции=1/2(ВС+АД)*h=(28+44)*15:2=540 кв см
3.S=1/2absinC=1*1*sin70=0,9397=0.46985 кв.м
4.S=absinC=2*3*sin70=5.6382 кв.м
1). АВСД - трапеция. АД = 60, ВС = 20, АВ = 13, СД = 37.S = ?
Проведем две высоты ВК и СР. тогда:
АК + РД = 60 - 20 = 40
Или из пр. тр-ов АВК и СДР:
кор(13^2 - h^2) + кор(37^2 - h^2) = 40, h = ВК = СР.
Решим уравнение относительно h:
169 - h^2 + 2кор((13^2 - h^2)(37^2 - h^2)) + 1369 - h^2 = 1600.
кор((13^2 - h^2)(37^2 - h^2))= h^2 + 31
(13^2 - h^2)(37^2 - h^2) = h^4 + 62h^2 + 961
1600h^2 = 230462
h^2 = 144
h = 12.
S = (АД+ВС)*h/2 = 80*6 = 480
ответ: 480 см^2.
2)АС = 39, АВ = СД = 17, АД = 44
Проведем высоты ВК и СР. Из пр.тр-ов АСР и СРД:
кор(39^2 - h^2) + кор(17^2 - h^2) = 44
1521 - h^2 + 289 - h^2 + 2кор((39^2 - h^2)(17^2 - h^2)) = 1936
кор((39^2 - h^2)(17^2 - h^2)) = h^2 + 63
(39^2 - h^2)(17^2 - h^2) = h^4 + 126h^2 + 3969
1936h^2 = 435600
h^2 = 225
h= 15
Тогда АК = РД = кор(17^2 - 15^2) = 8
Тогда ВС = АД - 2*8 = 44 - 16 = 28.
S = (АД+ВС)*h/2 = (44+28)*15/2 = 540
ответ: 540 см^2.
3) По формуле площади тр-ка:
S = (1/2) a^2 * sin70 = 0,5*0,93 = 0,47
ответ: 0,47 см^2.
4) По формуле площади пар-ма:
S = absin70 = 6*0,93 = 5,6
ответ: 5,6 см^2.
Чертеж прилагается. A - центр окружности. Отметим, что треугольник BCD - прямоугольный, так как угол CBD опирается на диаметр. Далее, известно, что хорда BK перпендикулярна диаметру CD. Пусть H - точка пересечения хорды и диаметра. Получается, что BH - высота в прямоугольном треугольнике, проведенная из вершины прямого угла (хотя это не так важно окажется). Также известно, хорда делится этим самым диаметром пополам. Это следует из того, что треугольник BAK - равнобедренный, так как AK=AB (радиусы), а AH - высота, проведенная к основанию (в смысле не к боковой стороне), но значит и медиана тоже. Тогда BH = 1/2 * BK = 12. Треугольник BHA - прямоугольный, по теореме Пифагора
CH = AC - AH =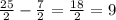
HD = AD + AH =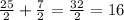
Теперь лишь из прямоугольных треугольников BHC и BHD по теореме Пифагора нужно найти BC и BD соответственно.
ответ: 15 и 20.