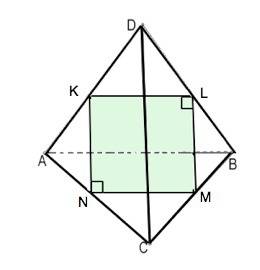
Ребра тетраэдра по условию равны, следовательно, он правильный и все его грани - правильные треугольники.
Каждая сторона сечения соединяет середины сторон такого треугольника и, как средняя линия соответствующей грани, равна половине параллельного ей ребра.
Скрещивающиеся ребра правильного тетраэдра перпендикулярны. DC⊥АВ⇒СD⊥MN, т.к. MN||АВ.
КN||CD⇒ KN⊥MN. Аналогично доказывается перпендикулярность всех соседних сторон сечения KLMN . Следовательно сечение- квадрат со стороной 38:2=19.
Площадь сечения 19²=361 (ед. площади)
Если гипотенуза с, катеты а и b, то
с²=a²+b²
169=25+b²
b=√(169-25)
b=√144=12
Треугольник с отношением сторон 5:12:13 часто встречается в задачах по геометрии (одно из так называемых Пифагоровых троек), стоит запомнить.