Теоремы (свойства параллелограмма):
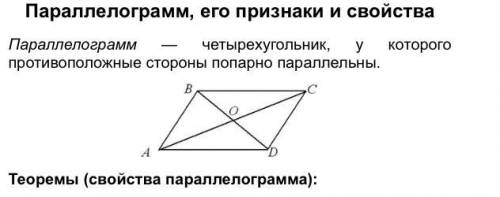
В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle
ADC,\angle BAD = \angle BCD.
Диагонали параллелограмма точкой пересечения делятся пополам: AO
= OC, OB = OD.
Углы, прилежащие к любой стороне, в сумме равны 180^\circ .
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.
Проведем CK║BD. Тогда DBCK - параллелограмм (противолежащие стороны попарно параллельны). ⇒ DK = BC, CK = BD = 8 см, AK = AD + BC
∠ACK = ∠AOD = 60° как соответственные при пересечении BD║CK секущей АС.
Из ΔАСК по теореме косинусов:
AK² = AC² + CK² - 2*AC*CK*cos60° = 25+64-2*5*8*1/2 = 89-40=49
AK = 7 см. ⇒ AD + BC = 7 см.
Продлим FN до пересечения с СК. NT = 1/2 DK как средняя линия ΔDCK ⇒ NT = 1/2 BC = FE (FE - ср. линия ΔABC)
Т.е. ET = FN = (AD + BC) /2 = 3,5 см