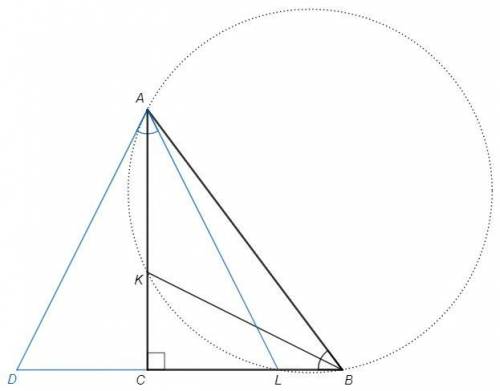
На продолжении BC отложим отрезок CD, равный СL.
В треугольнике DAL отрезок AC является высотой и медианой, следовательно и биссектрисой, треугольник равнобедренный.
DAL =2KAL =2∪KL/2 =2KBL =ABD
△DAL~△DBA (по двум углам) => △DBA - равнобедренный.
BC+CL =BC+CD =BD =BA =5
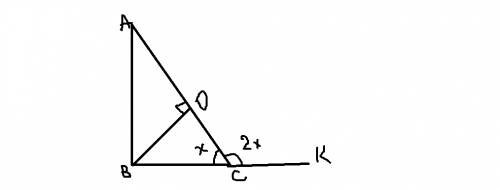
Пусть точки, делящие боковую сторону на 3 части называются М и К. Назовем параллельные основаниям прямые ММ1 и КК1. Рассмотрим трапеции АВСД и МВСМ1. Т.к. ММ1 || АД, а АВ - секущая к ним, то углы ДАВ и М1МВ равны. Аналогично доказываем, что угол АДС = ММ1С, значит эти трапеции подобные. Т.к. АК=КМ=МВ=АВ/3, то к-т подобия между трапециями МВСМ1 и АВСД = 1/3, т.е. ММ1:АД=1:3. Отсюда ММ1=14/3.
Аналогично трапеции КВСК1 и АВСД подобны с коэффицциентом 2/3, т.к. КВ:АВ=2:3. Значит КК1:АД=2:3, отсюда КК1=14*2/3=7/3
BK - биссектриса угла ABC, следовательно, ∠ABK = ∠KBC. Из точки K проведем перпендикуляр KD к стороне AB. ΔKDB = ΔCKB по гипотенузе и острому углу ⇒ BD = BC и KD = KC.
∠ABK опирается на дугу AK и ∠LBK опирается на дугу KL, то есть, хорды AK и KL опираются равные углы, поэтому AK = KL отсюда следует, что ΔKAD = ΔLCK по гипотенузе и катету ⇒ AD = CL, таким образом CB + CL = BD + AD = AB = 5