
Здесь следует рассмотреть сечение шара плоскостью, которая делит и шар,и конус таким образом, что все мы наблюдаем как бы в срезе. Смотри рисунок. Используем расширенную теорему синусов, чтобы узнать радиус описанной окружности вокруг треугольника АВС. Заметим, что этот треугольник равнобедренный. АВравно ВС как образующие конуса. Найдем АВ по теореме Пифагора
AB^2=AH^2+HB^2
AB^2=(3sqrt3)^2+3^2
AB^2=27+9
AB^2=36
AB=6 см.
Найдем противолежащий угол ВСА. Он равен углу ВАС.
По теореме синусов нам нужен синус этого угла.
sinangle BAC=frac{BH}{AB}
sinangle BAC=frac{3}{6}
sinangle BAC=frac{1}{2}
По теореме синусов
2R=frac{AB}{sinangle BCA}
2R=frac{6}{sinangle BAC}
2R=frac{6}{0,5}
2R=12
R=6 - радиус описанной окружности вокруг треугольника АВС, и радиус шара описанного вокруг конуса одновременно.
Объем шара находится по стандартной формуле
V=frac{4}{3}pi*R^3
V=frac{4}{3}pi*6^3
V=4pi*6^2*2
V=8pi*36
V=288pi
Sc = d²·tgα·√2/(2+tgα).
Sб = 4d²·tgα/(2+tgα).
So = d²/(2+tgα).
So =
Объяснение:
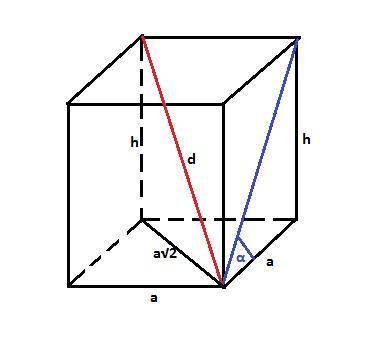
Призма правильная, значит в основании лежит квадрат. Пусть сторона квадрата равна "а". Тогда диагональ квадрата равна а√2.
Высота призмы равна h = a·tgα (из прямоугольного треугольника - половины боковой грани).
Квадрат диагонали призмы d² = h²+2a². (из прямоугольного треугольника - половины диагонального сечения).
d² = a²·tg²α+2a² = a²(2+tgα). => a = d/(√((2+tgα)).
h = a·tgα = d·tgα/(√((2+tgα)).
Тогда площадь диагонального сечения равна:
Sc = a√2·h = d√2/(√(2+tgα))·dtgα/(√(2+tgα)) = d²·tgα·√2/(2+tgα).
Площадь боковой поверхности равна произведению периметра основания на высоту призмы:
Sб = 4·a·h = 4d/(√((2+tgα))·d·tgα/(√((2+tgα)) = 4d²·tgα/(2+tgα).
Площадь основания (квадрата) равна квадрату стороны:
So = a² = d²/(2+tgα).
Відповідь:
Пояснення:
1) знаходимо перетин прямих МN i BC, так як вони лежать в одній площині АВС, нехай це буде точка Р
2) точка Р належить також площині ВСС1, так як пряма ВС лежить в цій площині, тому можемо провести пряму РК
3) знаходимо перетин прямої РК з ребрами, або їх продовженнями, СС1 та ВВ1
4) якщо маємо перетин РК з ребрами СС1 та ВВ1, нехай це точки Е та Н, то перерізом буде площина МNЕН
4а) якщо маємо перетин з продовженням ребра, нехай ВВ1, маємо точку Н, яка є перетином В1С1 і РК, а перетин РК з ребром СС1 є точка Е
Так як площини АВС і А1В1С1 паралельні, то будуємо пряму ТН║МN
ТН в перетині з В1А1 дає точку Т
перерізом є МNЕНТ