2√2 см.
Объяснение:
Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
Длина радиуса равна половине длины диагонали. Длина самой диагонали по теореме Пифагора равна √(4^2 + 4^2) = 4√2 см, тогда R = 1/2•4√2 = 2√2 (см).
Часто, понимая, что квадрат является правильным четырёхугольника, используют формулу
а4 = R√2, тогда
R = a4 /√2, где а4 - длина стороны квадрата.
В нашем случае
R = 4 /√2 = 2√2 (см).
1) Чтобы определить дос таточно найти длину АВ, АС, ВС
(Формула: 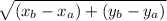
АВ=корень из ((1-0)^2+(-1-0)^2)=корень из (1+1)=корень из двух
ВС=корень из ((4-1)^2+(2-(-1))^2)=корень из (9+9)=корень из 18
АС=корень из ((4-0)^2+(2-0)^2))=корень из (16+4)=корень из 20
Если внимательно посмотреть, то мы увидим прямоугольный треугольник, с катетами АВ и ВС, гипотенузой АС. Можно это проверить теоремой Пифагора:
(корень из 2)^2+(корень из 18)^2=(корень из 20)^2
Все подходит, значит треугольник прямоугольный.
А под второй задачей неясно, что именно надо найти
1) Чтобы определить дос таточно найти длину АВ, АС, ВС
(Формула: 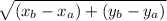
АВ=корень из ((1-0)^2+(-1-0)^2)=корень из (1+1)=корень из двух
ВС=корень из ((4-1)^2+(2-(-1))^2)=корень из (9+9)=корень из 18
АС=корень из ((4-0)^2+(2-0)^2))=корень из (16+4)=корень из 20
Если внимательно посмотреть, то мы увидим прямоугольный треугольник, с катетами АВ и ВС, гипотенузой АС. Можно это проверить теоремой Пифагора:
(корень из 2)^2+(корень из 18)^2=(корень из 20)^2
Все подходит, значит треугольник прямоугольный.
А под второй задачей неясно, что именно надо найти
2√2 см
Объяснение:
1) а=4 см
За теоремой Пифагора найдём d
R=4√2/2=2√2 см
2) a=4 см
R=(4×√2)/2=2√2 см