1.Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки
2.Треугольник называется разносторонним, если любые две стороны его не равны друг другу
3.Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине
4.Равносторонний треугольник - это треугольник у которого все стороны равны между собой, а все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
5.Остроугольный-если все его три угла острые т.е. меньше 90 градусов
6.Прямоугольный-треугольник,у которого есть прямой угол, т.е. угол, равный 90 градусам
7.Если один из углов треугольника тупой, то треугольник называется тупоугольным
Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что, 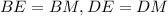 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что 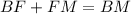 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть 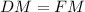 .
.
Учитывая доказанные равенства получаем,
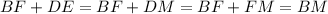
Что требовалось доказать.
! Сумма углов треугольника 180°
Угол С = 180° - 48° - 32° = 100°,
Угол С1 = углу С = 100°.
ответ: 100°.