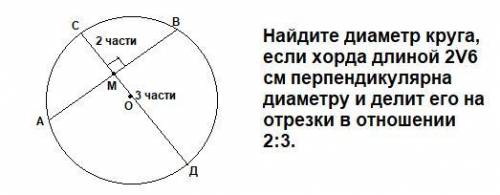
Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.
Объяснение:
ΔОМА=ΔОМВ как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)
По т. об отрезках пересекающихся хорд АМ*МВ=СМ*МД
Т.к. СМ/МД=2/3 , то МД=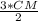 
. Получим √6*√6= СМ* .
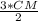СМ²=4, СМ=2 см .
Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).
d=5 см
=====================
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Відповідь: 60°.
Пояснення:Дано: коло з центром в точці О. AM i АК - дотичні (А поза колом).
М і К - точки дотику. ОА - перетинає коло в точці N. N - середина ОА.
Знайти: ∟MAK.
Розв'язання:
Виконаємо додаткові побудови: ОМ i ОК - радіуси.
За властивістю дотичних до кола маємо:
ОМ ┴ МА; ОК ┴ АК та МА = АК.
Розглянемо ∆ОМА та ∆ОКА - прямокутні.
ОА - спільна сторона; ОМ = ОК - радіуси.
За ознакою piвностi прямокутних трикутників маємо: ∆ОМА = ∆ОКА,
звідси маємо: ∟MAO = ∟KAO.
За аксіомою вимірювання кутів маємо ∟MAK = ∟MAO + ∟KAO = 2∟MAO.
Розглянемо ∆ОМА - прямокутний.
∟OMA = 90°; ОМ = ON = R; N - середина ОА; якщо ON = NA i ON = R, тоді ОА = 2R.
За властивістю катета, який лежить навпроти кута 30°, маємо, якщо ОМ = R
та ОА = 2R, тоді ∟MAO = 30°. Звідси маємо ∟MAK = 30° • 2 = 60°.
Biдповідь: 60°.
