Хотелось бы, конечно, чтобы вычисления оказались такими удобными. Но!
При данном пользователем решении в подобных треугольниках взяты отношения не соответственных сторон. Задача и впрямь тьма из-за вычислений - кругом дроби ))
При решении этой задачи нужно воспользоваться или теоремой
Пифагора, и тогда
h²=5² -х²
h²=12²-(13-х)²
5² -х²=12²-(13-х)²
Или воспользоваться этими правилами ( результат будет тот же)
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
По теореме Пифагора гипотенуза с=13 см
1-й отрезок гипотенузы
а²=а₁·с
25=а₁·13
а₁=25/13
2)1-й отрезок гипотенузы
b²=b₁*c
144=b₁*13
b₁=144/13
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
h ²=а₁·b₁ (25/13)·(144/13)=3600/169
h=60/13 см
При других значениях а и b ход решения тот же.
Надеюсь, при вычислениях не допустила ошибки.
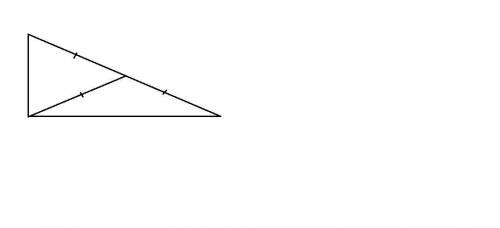
а) Любой прямоугольный треугольник можно разрезать на два равнобедренных треугольника.
Верно.
В любом прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине (см. рисунок). Если разрезать треугольник по медиане, то получим два равнобедренных треугольника.
б) Существует четырехугольник со сторонами 2, 3, 5, 11.
Неверно.
Каждая сторона четырехугольника должна быть меньше суммы остальных его сторон.
В данном четырехугольнике для стороны 11:
11 < 5 + 3 + 2 - неравенство неверно, значит четырехугольник с такими сторонами не существует.
в) В любом выпуклом пятиугольнике всегда есть тупой угол.
Верно.
Сумма углов выпуклого многоугольника определяется по формуле:
180°(n - 2), где n - количество сторон.
Для пятиугольника:
180° · 3 = 540°.
Если предположить, что все его углы острые (меньше 90°), то сумма будет меньше 90° · 5 = 450°. Значит есть тупой угол.
г) Внутри любого треугольника существует точка, равноудаленная от всех его вершин.
Неверно.
Точка, равноудаленная от всех вершин треугольника, - это центр описанной окружности.
Только в остроугольном треугольнике центр описанной окружности лежит внутри треугольника. В прямоугольном - на стороне (середина гипотенузы). В тупоугольном - вне треугольника.
здесь может быть только такие углы:
A= 70 градусов , B= 60 градусов, C= 50 градусов.!
Все сходится!)