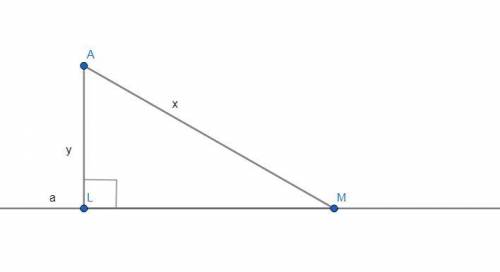
Чертёж смотрите во вложении.
Дано:
а - прямая.
АL - перпендикуляр от точки А до прямой а.
АМ - наклонная от точки А до прямой а.
∠ALM = 90°.
АМ+AL = 11 см.
Разность длин наклонной и перпендикуляра = 1 см.
Найти:
Расстояние от точки А до прямой а = ?
О каком расстоянии идёт речь в задании? Дело в том, что расстояние от точки до прямой - длина перпендикуляра, проведённого из этой точки к этой прямой. Поэтому, мы будем искать длину перпендикуляра AL.Так как АМ - наклонная, то она больше перпендикуляра AL (это не сложно доказать, если рассмотреть получившиеся прямоугольный ΔALM). Итак, поэтому, AM-AL = 1 см.Введём переменные. Пусть АМ = х, а AL = y. Составим систему линейных уравнений и решим её методом подстановки -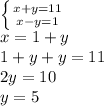
AL = y = 5 см.ответ: 5 см.
Объяснение:
vijohi8766
хорошист
20 ответов
2.9 тыс. пользователей, получивших
Смотри аналог с описанием решения (Если будет что-то не понятно, то пиши мне ❤️)
Объяснение:
Известна формула нахождения координат середины отрезка по координатам его концов:
xc = (xa + xb)/2, yc = (ya + yb)/2, где (xc; yc) – координаты точки С, которая является серединой отрезка AB.
В нашем примере даны координаты одного конца и середины отрезка. Воспользовавшись выше приведенной формулой преобразуем его для вычисления второго конца отрезка:
Xc = 2xb - xa, yc = 2yb - ya; xc = 2 * 6 - 6 = 6, yc = 2 * 6 – 4 = 8. C(6; 8).
Точка D — середина отрезка BC, поэтому xd = (xc + xb)/2, yd = (yc + yb)/2;
xd = (6 + 6)/2, yd = (8 + 6)/2; xd = 6, yd = 7. D(6;7).
ответ: C(6; 8); D(6;7).
