Объяснение:
Подробно.
В планиметрии если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Добавим - при условии, что третья прямая лежит в той же плоскости.
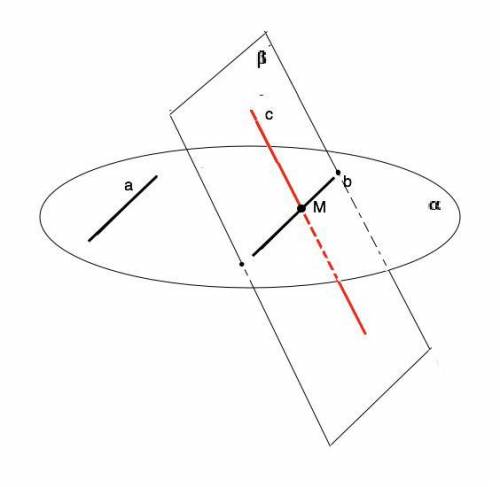
Пусть прямые а и b лежат в плоскости α, а прямая с, не лежащая в этой плоскости, пересекает прямую b в точке M.
Если одна из двух прямых (a) лежит в некоторой плоскости, а другая прямая (с) пересекает эту плоскость в точке (М), не лежащей на этой прямой, то эти прямые скрещивающиеся. Точка М не лежит на прямой а. Прямая с НЕ пересекает прямую а.
Отрезок ДМ - проекция диагонали ВД на основание АД, т.к. ВМ⊥АД и точка Д - общая.
В тр-ке АВМ АМ²=АВ²-ВМ²=5²-4²=9,
АМ=3 см,
ДМ=АД-АМ=11-3=8 см - это ответ.
В тр-ке ВМД ВД²=ВМ²+ДМ²=4²+8²=80,
ВМ=4√5 см.
sin(∠ВДМ)=ВМ/ВД=4/(4√5)=√5/5 - это ответ.