Площадь трапеции S=156 см²
Объяснение:
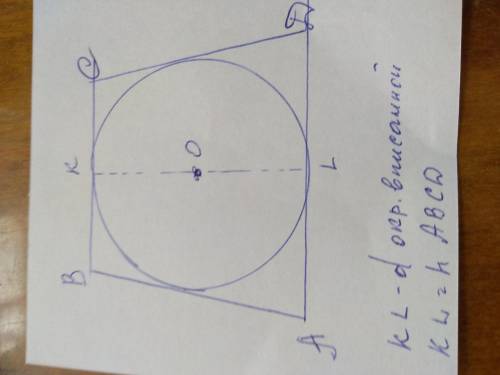
Окружность можно вписать в трапецию тогда и только тогда, когда сумма ее боковых сторон, равна сумме оснований т,е AB+CD= AD+BC
13+13=26см ( AD+BC ), отсюда - сумма оснований AB+CD=26см,
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=(а+b):2*h
Высота равнобокой трапеции АВСD равна диаметру вписаной окружности. Зная длинну вписанной окружности в трапецию АВСD, найдем ее диаметр по формуле: P=πd , где P-длинна окружности, которая по условию задачи равна 12πсм.
Подставляем известные значения в формулу и находим диаметр:
12π= πd
d =12π:π; d=12см
Площадь трапеции S=26:2*12=156 см²
Берешь раствор циркуля, равный радиусу, втыкаешь циркуль в любую точку на окружности, и отмечаешь 2 засечки на окружности.
Вставляешь циркуль в одну засечку и отмечаешь еще одну дальше.
И так далее. В итоге получаешь правильный 6-угольник.
Берешь точки через одну и получаешь правильный треугольник.
Восьмиугольник.
Рисуешь 2 диаметра, перпендикулярных друг к другу, получаешь квадрат.
Делишь каждую дугу пополам, получаешь правильный 8-угольник.
Чтобы разделить дугу пополам, нужно:
1) Сделать раствор циркуля явно больше половины угла.
2) Воткнуть циркуль в один конец дуги и нарисовать небольшую дугу.
3) Воткнуть циркуль в другой конец дуги и тоже нарисовать дугу.
4) Эти две дуги пересекутся в какой-то точке.
5) Соединяешь центр круга с этой точкой, получаешь биссектрису.
Она делит пополам угол и дугу.