Противоположные углы параллелограмма равны между собой, соседние углы параллелограмма в сумме равны 180°.
∠A=∠C; ∠B=∠D; ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°
1) Острый угол параллелограмма равен 46°
∠A = 46°; ∠B = ∠D = 180° - 46° = 134°
∠A = ∠C = 46°; ∠B = ∠D = 134°
2) Так как сумма двух углов 186° больше 180°, значит, это сумма двух тупых углов параллелограмма.
∠B + ∠D = 186°; ∠B = ∠D = 186° : 2 = 93°
∠A = ∠C = 180° - 93° = 87°
3) Тупой угол параллелограмма на 56° больше острого угла.
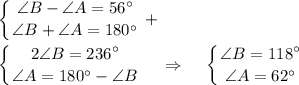
∠A = ∠C = 62°; ∠B = ∠D = 118°
4) Острый угол параллелограмма в 3 раза меньше тупого угла.
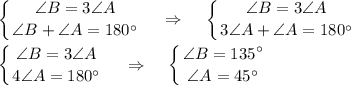
∠A = ∠C = 45°; ∠B = ∠D = 135°
5) Острый угол относится к тупому углу как 5:7
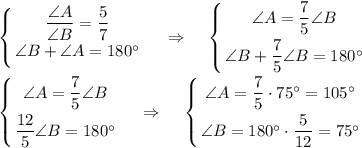
∠A = ∠C = 75°; ∠B = ∠D = 105°
Треугольник самая распространенная фигура. В лесу, когда мы смотрим на ель и ее тень, то перед нами представляется равнобедренный треугольник.
На магических символах.
Предметы обихода: треуголки, вырезы на одежде.
Музыкальные инструменты.
ТРЕУГОЛЬНИК, самозвучащий музыкальный инструмент — стальной прут, согнутый в виде треугольника, по которому ударяют палочкой. Применяется в оркестрах и инструментальных ансамблях.
“Египетский” треугольник
Среди бесконечного количества возможных прямоугольных треугольников, особый интерес всегда вызывали так называемые «пифагоровы треугольники», стороны которых являются целыми числами. Несомненно, «пифагоровы треугольники» также относятся к разряду «сокровищ геометрии», а поиски таких треугольников представляют одну из из интереснейших страниц в истории математики. Наиболее широко известным из них является прямоугольный треугольник со сторонами 4, 3 и 5. Он назывался также «священным» или «египетским», так как он широко использовался в египетской культуре