Прямая параллельная основаниям трапеции abcd , пересекает ее боковые стороны ab и cd в точках e и f - id692158920230523 от Оленька090 23.05.2023 13:55

Question

Геометрия: Прямая параллельная основаниям трапеции abcd , пересекает ее боковые стороны ab и cd в точках e и f соответственно. найдите отношение отрезков cf : df , если ad=15 , вc=12, ef=21

Оленька090 · Accepted Answer

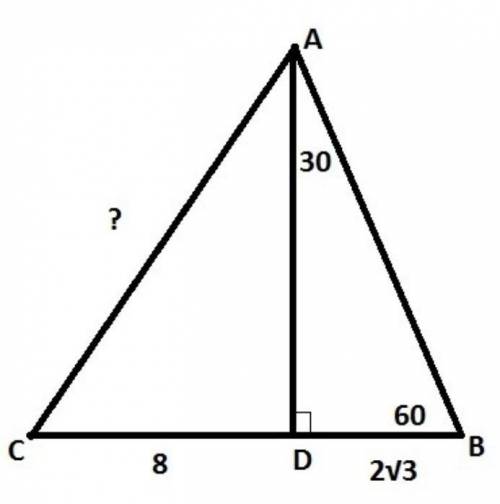
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.

Объяснение:

Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=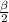 $\frac{\beta }{2}$ .

ΔАОК- прямоугольный ,

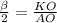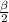cos $\frac{\beta }{2} =\frac{KO}{AO}$ , KO=R*cos $\frac{\beta }{2}$ ;

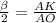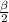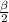sin $\frac{\beta }{2} =\frac{AK}{AO}$ ,AK=R*sin $\frac{\beta }{2}$ ,AB=α2Rsin $\frac{\beta }{2}$ .

ΔSKO прямоугольный ,cos α=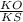 $\frac{KO}{KS}$ , KS=R*cos 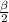$\frac{\beta }{2}$ /cosα.

S=0,5*AB*SK ,S=0,5*2R*sin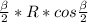 $\frac{\beta }{2} *R*cos\frac{\beta }{2}$ / cosα,

S=0,5*R²*sinβ/cosα=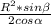 $\frac{R^{2} *sin\beta }{2 cos\alpha }$

Прямая параллельная основаниям трапеции abcd , пересекает ее боковые стороны ab и cd в точках e и f соответственно. найдите отношение отрезков cf : df , если ad=15 , вc=12, ef=21

MOGZ ответил