ответ: диаметр ВН=10см
Объяснение:
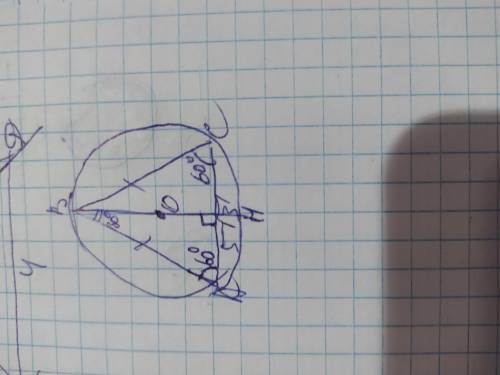
Проведём из вершины В высоту ВН. Она проходя через треугольник АВС будет являться искомым диаметром. Так как ∆АВС равнобедренный, то углы при основании будут равны, поэтому <А=<С=60°. Сумма углов треугольника составляет 180°, поэтому
<В=180–60–60=60°. Все углы этого треугольника равны, поэтому он является равносторонним и АВ=ВС=АС=5√3см.
Радиус описанной окружности вокруг равностороннего треугольника вычисляется по формуле:
R=a/√3, где а - сторона треугольника:
R=5√3÷√3=5см;. R=BO=OH
Тогда диаметр ВН=2×5=10см
Я не уверена с правильным ответом. ну все же
С тупых углоа В и Д я провела бисектрисы ВК и ДМ. АК = МС = 17 см, КД = ВМ = 12см.
Угол В = углу Д, то значит бисектрисы поделят их на четыре равных угла:
Уголы АВК = КВС = АДМ = СДМ.
Так как это параллелогамм, то бисектрисы будут равны и паралельные.
Посмотри угол АДМ и угол АКВ они будут равны как относительные.
Отсюда вывод, если угол АВК = углу АКВ, значит теугольник АВК равнобедренной.
Где АК = АВ = 17см.
АВ = СД = 17 см
АД = ВС = 17 + 12 = 29
Р = 17 + 17 + 29 + 29 = 92 см
Равнобедренный - другие углы (BAK и BCK) по 45
Медиана в нем и биссектриса и высота (BK)
Медиана образует два равнобедренных треугольника (ABK и CBK)
Следовательно: AK=KC=4
Отсюда AC=AK+KC=8
По теореме Пифагора стороны AB и BC - гипотенузы,
следовательно они равны =V4^2+4^2=V16+16=V32=приблизительно 5,7