1. 13
Объяснение:
1.
Проведём FH перпендикулярно DE следовательно треугольник FHE прямоугольный.Треугольник DCE прямоугольный следовательно треугольник FCE тоже прямоугольный.
EF- биссектриса следовательно угол 1 = углу 2.Следовательно FHE= FCE(по острому углу) следовательно FH=FC=13
ответ: 13
2.
Строим острый угол В. Из вершины угла проводим окружность радиусом равным катету, и отмечаем точку пересечения А. Так как треугольник — прямоугольный, то восстанавливаем перпендикуляр из точки А. Полученная точка пересечения С. Соединяем попарно вершины треугольника. Искомый треугольник построен.
(Рисунок в закрепе)
3.
ответ: 6,72
Объяснение: Ортотреугольником называют треугольник, вершинами которого являются основания высот некоторого треугольника.
* * *
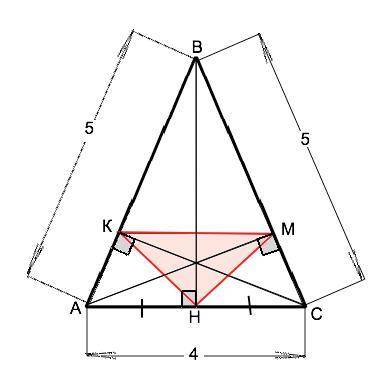
На рисунке точки К, М и Н - основания высот треугольника АВС. ⇒ ∆КМН - его ортотреугольник.
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. ⇒ АН=СН=4:2=2.
Прямоугольные ⊿ АКС=⊿ СМА по равному острому углу ( ∠А=∠С как углы при основании равнобедренного треугольника) и общей гипотенузе АС.
Медианы прямоугольных треугольников равны половине гипотенузы.. КН=МН=4:2=2. Следовательно, АН=КН, СН=МН, – ∆ АКН и ∆ СМН равнобедренные, при этом углы при их основаниях равны углам при основании ∆ АВС. Поэтому
∆ АКН и ∆СМН подобны ∆ АВС.
Из подобия следует НС:ВС=МС:АС ⇒ 2:5=МС:4, откуда МС=8/5=1,6
ВК=ВМ=ВС-СМ=5-1,6=3,4
∆ КВМ~∆ АВС ( оба равнобедренные с общим острым углом В) ⇒
ВК:АВ=КМ:АС ⇒ КМ=3,4•4:5=2,72
Р(КМН)=КМ+КН+МН=2,72+2+2=6,72 ( ед. длины)
К тому же медиана-высота-биссектриса делит ΔABC на два равных треугольника: ΔABD и ΔCBD.
1) Боковые стороны найдём по теореме Пифагора:
AB² = BD² + AD² = 25 + 144 = 169
АВ = 13
2) sinA = sinC =
3) Найдём площадь:
SΔABC =
Эту же площадь можно выразить через боковую сторону и высоту проведенную к ней. Формула та же:
h боковая ΔABC =
Удачи!