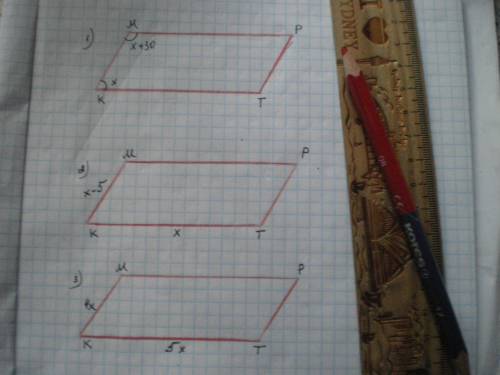
1. Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠К=х°, тогда ∠М=х+30°. Составим уравнение:
х+х+30=180; 2х+30=180; 2х=150; х=75.
∠К=75°, ∠М=75+30=105°.
∠Р=∠К=75°; ∠Т=∠М=105° как противолежащие углы параллелограмма.
2. Полупериметр р (КМРТ)=400:2=200 см. Пусть КТ=х см, тогда КМ=х-5 см. Составим уравнение:
х+х-5=200; 2х=205; х=102,5;
КТ=102,5 см; КМ=102,5-5=97,5 см;
МР=КТ=102,5 см;
РТ=КМ=102,5-5=97,5 см. (как противолежащие стороны параллелограмма)
3. Периметр КМРТ=180 см. Пусть КМ=4х см, КТ=5х см. Составим уравнение:
(4х+5х)*2=180; 9х*2=180; 18х=180; х=10.
КМ=10*4=40 см, КТ=10*5=50 см; РТ=КМ=40 см; МР=КТ=50 см. (как противолежащие стороны параллелограмма).
АК - биссектриса.
АВ²=АС²+ВС²=45²+12²=2169,
АВ=3√241.
По теореме биссектрис АС/АВ=СК/ВК.
Пусть СК=х, ВК=12-х.
45/х=3√241/(12-х),
540-45х=3х√241,
3х(√241+15)=540,
х=180/(√241+15)≈5.9
СК=5.9, ВК=12-5.9=6.1,
АК²=АС·АВ-СК·ВК=45·3√241-5.9·6.1≈2059.8,
АК=≈45.4 - это ответ.