Периметр правильного n-угольника равен p, а сторона аn. радиус окружности, описанного около этого n-угольника, равен r, а радиус окружнасти, вписанной в него,равен r. найдите неизвестные элементы многоугольника по следующим данным: n=6 r=9см.
1. Большее основание на 30 больше меньшего. Так как трапеция равнобедренная, эти 30 распределяются по 15 у одной боковой стороны и у другой. 2. Найдём высоту (перпендикуляр, опущенный из вершины меньшего основания на большее). Имеем прямоугольный треугольник, в котором гипотенуза = 39, один катет = 15 (см. пункт 1). Высота = второй катет этого треугольника. 39^2 - 15^2 = 1296 = 36^2 Высота = 36. 3. Теперь имеем прямоугольный треугольник, в котором диагональ трапеции - гипотенуза, высота - один катет, а второй катет = меньшее основание + 15 = 77. 77^2 + 36^2 = 5929 + 1296 = 85^2. Диагональ = 85
1. Большее основание на 30 больше меньшего. Так как трапеция равнобедренная, эти 30 распределяются по 15 у одной боковой стороны и у другой. 2. Найдём высоту (перпендикуляр, опущенный из вершины меньшего основания на большее). Имеем прямоугольный треугольник, в котором гипотенуза = 39, один катет = 15 (см. пункт 1). Высота = второй катет этого треугольника. 39^2 - 15^2 = 1296 = 36^2 Высота = 36. 3. Теперь имеем прямоугольный треугольник, в котором диагональ трапеции - гипотенуза, высота - один катет, а второй катет = меньшее основание + 15 = 77. 77^2 + 36^2 = 5929 + 1296 = 85^2. Диагональ = 85
Дано: правильный многоугольник,
n = 6, r = 9 см.
Найти: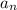 , P, R.
, P, R.
a₆ = 2 · 9 · tg30° = 18 / √3 = 6√3 см
Р = 6 · а₆ = 36√3 см
В правильном шестиугольнике радиус описанной окружности равен стороне:
R = a₆ = 6√3 см