Zmeura1204
Объяснение:
1)
Дано:
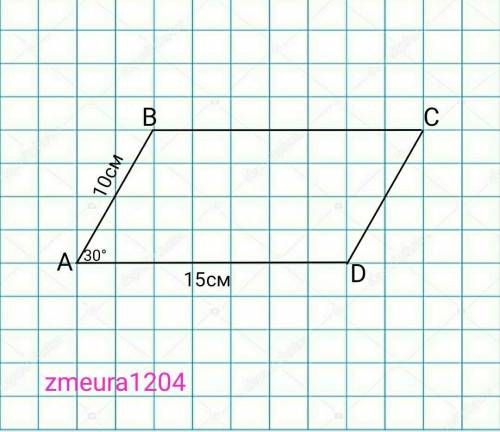
АВСD-параллелограм
AB=10см
AD=15см
<А=30°
S=?
_______
Решение
S=AB*AD*sin<A
sin<30°=1/2
S=1/2*10*15=75см²
ответ: 75см²
2)
Дано:
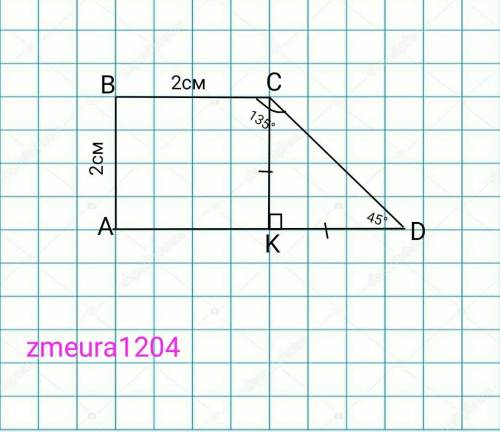
ABCD- трапеция
<ВАD=<ABC=90°
<BCD=135°
BC=2см
АВ=2см
S(ABCD)=?
______
Решение
Сумма углов прилежащих к боковой стороне трапеции равна 180°
<CDK=180°-<BCD=180°-135°=45°
Проведём высоту СК.
∆CKD- прямоугольный равнобедренный треугольник (углы при основании равны. <СКD=90°; <CDK=45°; <KCD=90°-45°=45°)
CK=KD=AB=2см
АD=BC+KD=2+2=4см.
S(ABCD)=CK(BC+AD)/2=2(2+4)/2=6см²
ответ: 6см²
9 м и 12 м
Объяснение:
Пусть х - это гипотенуза, тогда (х-3) и (х-6) - катеты.
Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов:
х² = (х-3)² + (х-6)²
х² = х² - 6х + 9 + х² - 12х + 36
х² = 2х² - 18х + 45
х² - 18х + 45 = 0
х₁,₂ = 9 ±√(81-45) = 9 ±√36 = 9±6
х₁ = 9 + 6 = 15
х₂ = 9 - 6 = 3
Из полученных значений условию задачи удовлетворяет только х = 15 м, т.к. длины катетов могут быть выражены только положительными числами.
Следовательно, катеты прямоугольного треугольника равны:
15 - 3 = 12 м и 15 - 6 = 9 м
ПРОВЕРКА:
12² + 9² = 144 + 81 = 225 - сумма квадратов катетов;
15² = 225 - квадрат гипотенузы;
225 = 225 - следовательно, задача решена верно.
ответ: катеты прямоугольного треугольника равны 9 м и 12 м.
1. Радиус окружности, описанной около правильного треугольника:
R = a₃√3/3 = 5√3 · √3/3 = 5 см.
Эта же окружность вписана в правильный шестиугольник. Тогда сторона правильного шестиугольника:
a₆ = 2r · tg(180°/6) = 2r · tg30° = 2r · √3/3
r = R = 5 см
a₆ = 2 · 5 · √3/3 = 10√3/3 см
2. R = 2√3 см, r = 3 см
Запишем формулы стороны правильного многоугольника через радиус описанной и вписанной окружности, получаем систему уравнений с двумя неизвестными: а и n.
a = 2R · sin(180°/n) = 4√3 · sin(180°/n) (1)
a = 2r · tg(180°/n) = 6 · tg(180°/n) (2)
Приравниваем правые части:
4√3 · sin(180°/n) = 6 · tg(180°/n), и так как tgα = sinα/cosα, получаем:
2√3 · sin(180°/n) = 3 · sin(180°/n)/cos(180°/n)
Делим на sin(180°/n) обе части уравнения:
2√3 = 3/cos(180°/n)
cos(180°/n) = 3 / (2√3) = 3√3/6 = √3/2, ⇒
180°/n = 30°
n = 180°/30° = 6 - количество сторон многоугольника.
Для правильного шестиугольника сторона равна радиусу описанной окружности: а = R = 2√3 см.
Или подставляем найденное значение в формулу (1) или (2):
a = 6 · tg(180°/n) = 6 · tg(180°/6) = 6 · tg30° = 6/√3 = 2√3 cм