Я уже делал такую задачу, там сторона была 4*корень(2); но я решение почти до конца делаю в общем виде, если что не так - подставьте свое значение.
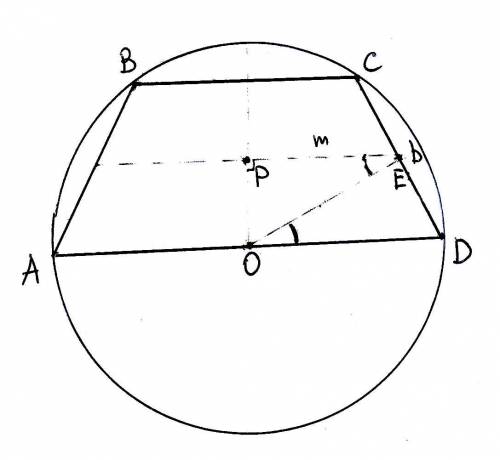
Рассмотрим два подобных прямоугольных треугольника ОРЕ и ОЕD; РО препендикулряно РЕ, РЕ - половина средней линии m = 14; OD = R - радиус окружности, ED = CD/2 = b/2, где b = 4*корень(2) - боковая сторона.
EP/OE = OE/OD; OD*EP = OE^2 = OD^2 - ED^2;
R^2 - R*m/2 - (b/2)^2= 0;
R^2 - R*7 - 8 = 0; (R - 8)*(R + 1) = 0; R = 8 (второй корень -1 отброшен)
Для особо одаренных :))) привожу то решение, которое я нашел вначале.
Пусть угол РЕО = угол EOD = Ф; тогда
ОЕ = R*cos(Ф); m/2 = OE*cos(Ф); m/2 = R*(cos(Ф))^2 = R*(1 - (sin(Ф))^2);
R*sin(Ф) = (b/2); sin(Ф) = b/(2*R);
m/2 = R*(1 - (b/(2*R))^2;
В этой задаче только одна тонкость - 140 градусов - это угол при вершине. Поэтому угол при основании равен Ф = (180 - 140)/2 = 20 градусов (или пи/9).
Осталось вспомнить теорему синусов 2*R*sin(Ф) = a; а = 10;
R = 5/sin(пи/9); само собой, это можно вычислить только приближенно (если только учитель не садист :) но в любом случае, это за пределами всех школьных программ)
R = 5/0,342020143325669 = 14,6190220008154; (слава Гейтсу, есть Excel)
Вот, чего только не узнаешь, ковыряясь в тривиальных задачах. Оказывается, тригонометрические функции угла 20 градусов теоретически невозможно выразить в радикалах. Оказывается, это противоречит некоей теореме Гаусса, согласно которой с циркуля и линейки можно построить не любой правильный n-угольник, а только для некоторых n, и 18-угольники в это разрешенное множество не входят. В частности, можно выразить в радикалах функции всех углов, кратных 3 градусам.
Однако это не означает, что cos(пи/9) (или синус, не важно) нельзя "вычислить на кончике пера". Легко видеть, что
cos(60) = 4*(cos(20))^3 - 3*cos(20); если x = cos(20); то
x^3 - (3/4)*x - 1/8 = 0;
У этого уравнение есть по крайней мере один действительный корень (равный косинусу 20 градусов, конечно). Есть формулы Кардано для решения в радикалах таких уравнений. Но - вот беда - результат, хоть и действительный, и будет выражен в радикалах, обязательно будет содержать внутри записи мнимую единицу i; i^2 = -1; и избавиться от неё в выражении никак не получится (в противном случае нарушилась бы та самая теорема Гаусса). : это я так - развлекаюсь :)))
1). FO=OK, т.к. O - середина FK
2). MO=ON, т.к. O - середина MN
3). ∠FOM=∠KON, как вертикальные углы
Из равенства треугольников следует равенство соответствующих элементов, а именно ∠FMN=∠KNM. Так как при секущей MN накрест лежащие углы ∠FMN и ∠KNM равны, то прямые FM и KN параллельны, что и требовалось доказать.