Найти площадь правильного треугольника, если расстояние от его центра до вершины = 4 метра

👇

Ответ:

malikamalik1406

20.02.2022

Итак, рассмотрим треугольник ABC. Центром правильного треугольника является как центр вписанной, так и центр описанной окружностей. Центр описанной окружности равноудален от вершин треугольника, то есть те 4 метра, которые нам даны, есть не что иное, как радиус описанной окружности. Теперь воспользуемся следующей универсальной формулой площади треугольника: S abc = (AB*BC*AC)/(4R), где R-радиус описанной окружности, то есть R=4, также учтем, что наш треугольник правильный, т.е. все его стороны равны между собой, тогда получим следующий вид этой формулы S abc = (AB³)/16. Также вспомним еще одну из формул площади треугольника: S abc = 1/2*AB*BC*sin(∠ABC). Зная что все стороны равны, а все углы в треугольнике по 60 градусов, получаем: S abc = 1/2*(AB²)*sin(60°) = 1/2*(AB²)*(√3)/2. Теперь сопоставим две полученные формулы площадей: (AB³)/16=1/2*(AB²)*(√3)/2. Домножим обе части на 16: AB³=4*(√3)*(AB²), разделим обе части на AB², AB=4*(√3). Теперь подставим это значение в любую из формул площади: S abc = (AB³)/16 = 64*3*(√3)/16 = 12*(√3) м² . ответ: 12*(√3) м²

Найти площадь правильного треугольника, если расстояние от его центра до вершины = 4 метра

Найти площадь правильного треугольника, если расстояние от его центра до вершины = 4 метра

4,4(79 оценок)

Открыть все ответы

Ответ:

Анна157211цаа

20.02.2022

144√3

Объяснение:

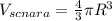
$V_{scnara} =\frac{4}{3} \pi R^{3}$

по условию известно, что Vшара=32π√3

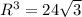
$R^{3} =24\sqrt{3}$

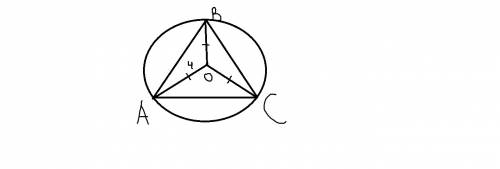
2. по условию известно, что шар вписан у правильную треугольную призму, следовательно шар касается граней призмы:

а). оснований призмы, => высота призмы H =2R

б). боковых граней призмы, точки касания - точки пересечение диагоналей боковых граней, => диаметральное сечение шара +призма = круг, вписанный в правильный треугольник

R радиус окружности, вписанной в правильный треугольник:

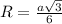
$R=\frac{a\sqrt{3} }{6}$

сторона правильного треугольника :

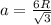
$a=\frac{6R}{\sqrt{3} }$

3. объём призмы вычисляется по формуле:

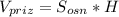
$V_{priz} =S_{osn} *H$

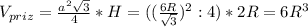
$V_{priz} =\frac{a^{2}\sqrt{3}}{4} *H=((\frac{6R}{\sqrt{3} } )^{2} :4)*2R=6R^{3}$

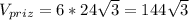
$V_{priz} =6*24\sqrt{3} =144\sqrt{3}$

4,6(14 оценок)

Ответ:

mizery1

20.02.2022

Треугольник со сторонами 13,14 и 15 см вращается вокруг средней стороны.Найти поверхность тела.

Тело вращения будет походить на детскую игрушку юла.

Т.е. верхняя и нижняя части - два конуса с общим основанием АА₁ и радиусом, равным высоте АО данного треугольника, проведенным к средней по величине стороне, равной 14 см.

Чтобы найти эту высоту, нужно найти по формуле Герона площадь треугольника. Вычисления приводить не буду - треугольник с такими сторонами встречается в задачах часто, его площадь легко запоминается и равна 84 см²

S=a*h:2, где а - сторона, h- высота к ней.

2S=a*h

h=2S:а

h=168:14=12 см - это радиус окружности - общего основания конусов.

Рассмотрим рисунок.

Площадь тела равна сумме площадей боковых поверхностей конуса АВА₁ и конуса АСА₁

S =πrl

S₁=π*12*13

S₂=π*12*15

S общ=12π(13+15)=336 π

при π=3,14

S=1055,04см²