ответ: 5:3
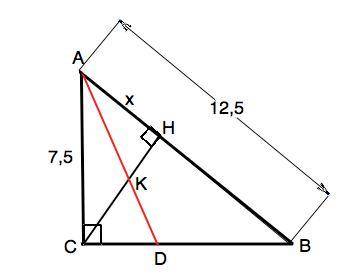
Объяснение: Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Обозначим точку пересечения биссектрисы АD и высоты СН буквой К. Тогда СК:КН=АС:АН.
В прямоугольном треугольнике катет есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
АС - катет, АН его проекция на гипотенузу. Примем АН=х ⇒ АС²=АВ•АН ⇒ 7,5²=12,5•х, откуда х=4,5
Искомое отношение СК:КН=7,5:4,5=5:3

с² = 5²+6²-2*5*6*cos 28° = 25+36-60* 0.882948 = 8.023144.
c = √ 8.023144 = 2.832516.
sin A = 5*sin 28°/c = 5* 0.469472/ 2.832516 = 0.828718.
<A = arc sin 0.828718 = 0.976814 радиан = 55.96731°.
<B = 180°-<C-<A = 180°-28°-55.96731° = 96.03269°.