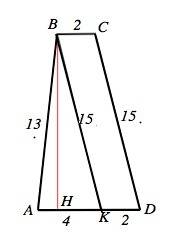
Обозначим трапецию АВСD.
АВ=13 см, СD=15 см, ВС=2 см, AD=6 см. ВН - высота трапеции.
Через вершину В проведем ВК параллельно СD.
Противоположные стороны четырехугольника КВСD параллельны – КВСD - параллелограмм, KD=ВС=2 см
Тогда АК=4 см.
Площадь ∆ АВК по ф. Герона , где р - полупериметр,
равна √(p•(p-AB)•(p-BK)•(p-AK)=√16•3•1•12)=24 см²
ВН =высота трапеции=высота ∆ АВК.
Из формулы площади треугольника
h=2S:a, где а- сторона, к которой высота проведена.
ВН=48:4=12 (см)
Площадь трапеции равна произведению высоты на полусумму оснований.
S(ABCD)=12•(2+6):2=48 см*
а)  D , следовательно, AC — биссектриса угла BAD
б) Поскольку BA = BD = BC = 8,5. точки A , D и C лежат на окружности радиуса 8,5 с центром в точке B.
Продолжим основание BC за точку B до пересечения с этой окружностью в точке E. Тогда
EC — диаметр окружности, а ADCE — равнобедренная трапеция. Поэтому AE = СD, а так как точка A лежит на окружности с диаметром CE , получаем, что 
Из прямоугольного треугольника CAE находим, что 
Следовательно, CD AE = 8. ответ: 8