АВ=13; EF=8
Объяснение:
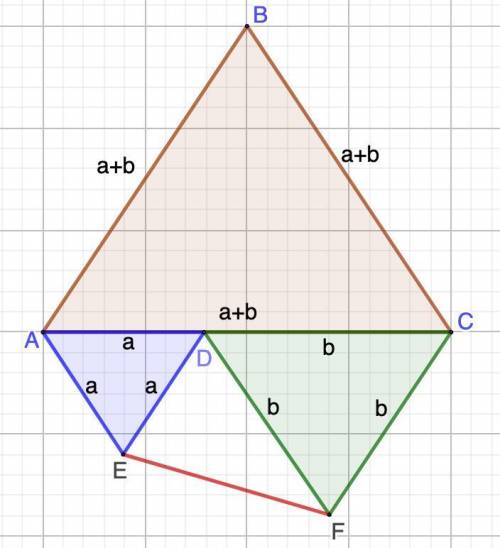
Дано: ΔАВС - равносторонний;
Δ ADE и ΔDCF - равносторонние
Р (ΔDEF) = 21
P (ABCFE) = 47
Найти: АВ; EF
Треугольники равносторонние ⇒ у них все стороны равны.
Пусть сторона ΔAED равна a, а сторона ΔDCF равна b.
⇒ сторона ΔАВС равна a+b.
1. Рассмотрим ΔEDF.
P (ΔEDF) = 21 ⇒ EF =21 - (a+b) = 21 - a - b
2. Рассмотрим ABCFE.
Р (ABCFE) = 47
Периметр - сумма длин всех сторон.Р (ABCFE) = AB + BC + CF + EF +AE
47 = a+b+a+b+b+21-a-b+a
47 = 2a +2b +21
2(a+b) = 26
a+b = 13
3. АВ = a+b = 13
EF = 21 - (a+b) = 21 -13 = 8
Объяснение:
1 В равнобедренном треугольнике медиана является биссектрисой и высотой, BD медиана по усл, а так как угол BDC прямой то BD является также и высотой треугольника ABC, следует медиана и высота совпадают значит этот треугольник равнобедренный что и требовалось доказать
2 пусть х = боковой стороне, тогда основание = x +3, зная, что периметр треугольника равен 45 см, составим уравнение
2x + x +3 = 45
3x = 42
x= 14
2) Основание равно x + 3 = 14 +3 = 17 cм
ответ: 14, 14, 17 см.
больше не знаю
P - периметр
ab=(P-(ad+bc))/2=10
bh=ab*sin=10*0.4=4