Пирамида SABCD пересечена плоскостью KLNM, параллельной основанию.
1. Каково взаимное расположение прямых (пересекаются, скрещиваются, параллельны):
а) AS и CD? ответ: скрещиваются, т.к. CD∈( ADC) , AS∩( ADC) =A , A∉CD
б) AB и KL? ответ: параллельны , т.к. (KLN)||(АВС).
в) CD и LM? ответ: скрещиваются, т.к.CD∈(CDM) , а LM пересекает эту плоскость в точке М , не лежащей на CD.
2. Как расположены плоскости:
а) ASB и DSC? ответ: пересекаются ,т.к. имеют общую точку
б) ABD и ASD? ответ: пересекаются ,т.к имеют общую прямую.
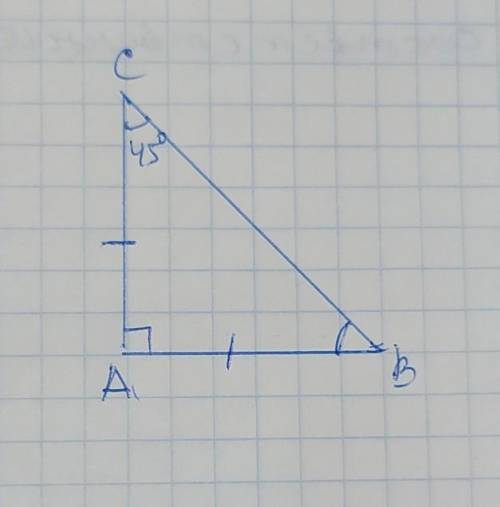
УголА=90°
Объяснение:
в прямоугольном треугольнике сумма острых углов составляет 90°, поэтому второй острый угол равен 90–45=45°. Следовательно этот треугольник равнобедренный поскольку острые углы в нём равны и каждый составляет 45°, поэтому и катеты этого треугольника равны. Теперь выясним какой именно угол равен 90°. Так как катеты равны, то самая большая сторона - это гипотенуза.
ВС=8√6см. √6≈2,4, тогда ВС=8×2,4=19,2см, (ВС=19,2см > АВ=13см), значит ВС - гипотенуза, лежащая напротив прямого угла А, при этом АВ=АС - (катеты), уголВ=уголС=45°