Решить . №1 радиусы двух окружностей равны 3см и 8см. найдите растояние мужду их центрами если окружности имеют: 1) внутреннее косание 2) внешнее косание №2 расстояние между цунтрами двух окружностей если их радийсы равны: 1) 7см и 5см 3) 10см и 5см 2) 16см и 2см 4) 7см и 7см наверно лёгкие , но я их не могу решить, я не была в школе (болела) учитель не будет учить и повторять сомной всё что класс уже так что .

👇

Ответ:

OskarWild

14.01.2021

Первый и второй номер решается по одинаковым формулам, если я тебя правильно понял.
для того, чтобы найти расстояние между центрами окружностей со внутренним касанием нужно вычесть из большего радиуса меньший.
для нахождения расстояния между окружностями со внешним касанием необходимо сложить два данных радиуса.

Во втором задание ты не написала как окружности расположены, поэтому я составил таблицу:
первая колонка- номер вопроса
вторая колонка- а) внутреннее касание
третья - б) внешнее касание.
и дальше по строкам решение с ответом для каждого касания.

Решить . №1 радиусы двух окружностей равны 3см и 8см. найдите растояние мужду их центрами если окруж

Решить . №1 радиусы двух окружностей равны 3см и 8см. найдите растояние мужду их центрами если окруж

4,4(40 оценок)

Открыть все ответы

Ответ:

annamironenkosp0dly3

14.01.2021

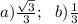
$a) \frac{\sqrt{3} }{3}; ~~b) \frac{1}{3}$

Объяснение:

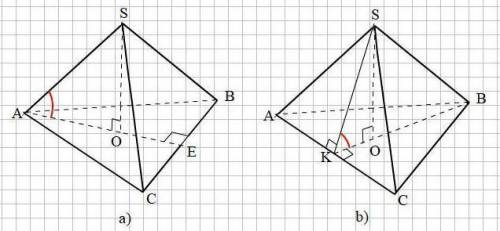
Смотри прикреплённый рисунок.

Пусть а = 8 см - ребро тетраэдра

a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;

Опустим высоту SO на плоскость АВС.

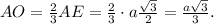
$AO=\frac{2}{3} AE = \frac{2}{3}\cdot a\frac{\sqrt{3} }{2} = \frac{a\sqrt{3} }{3}.$

Угол между прямой SA и плоскостью АВС есть угол SAO

b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;

Опустим высоту SO на плоскость АВС.

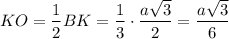
$KO= \dfrac{1}{2} BK = \dfrac{1}{3}\cdot \dfrac{a\sqrt{3} }{2} =\dfrac{a\sqrt{3} }{6}$

Проведём в грани SAC апофему SK = 0,5а√3

Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС

Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.

ГЕОМЕТРИЯ ОДНО ЗАДАНИЕ Дан правильный тетраэдр SABC. Выполните рисунок. Найдите: а) косинус угла меж

4,4(85 оценок)

Ответ:

вета18С

14.01.2021

Дано :  <ABC = <ABD =<CBD =90; AB =1 ; BC =3 ; CD =4 .
1)
а) проекцию BD на плоскость ABC = 0, т.к . BD  ┴ (ABC)   DC┴ BA DC ┴ BC);
б) AB ┴ (DBC) т.к . AB┴ BD  и AB┴ BC.
Значит   <ADB это   угол между прямой AD и плоскостью DBC
следовательно   :
  из ΔADB :     sin (<ADB) =AB/AD .
ΔCBD :    DB = √(DC² -BC²) =√(4² -3²) =√7.
ΔABD : AD =√(DB² +AB²) =√(7 +1) =2√2 .

sin (<ADB) =AB/AD =1/(2√2) =(√2 ) /4 .

г) (BCD) перпендикулярно (BCA)
BCD проходит по прямой BD    которая   ┴( ABC) .

2) ABCD_ ромб ;
AB=BC =CD =DA = BH =b ; < A =< C =60° ; HB ┴(BAC) или тоже самое
HB ┴(ABCD)
а) Определите угол между плоскостями: BHC и DBY .
Y --- неизвестно
Определить угол между плоскостями: BHC и DBH :
(BHC) ^ (DBH) = <DBE =60° . DB ┴ BH ,CB┴ BH   лин.  угол [ HB ┴((ABCD)⇒HB ┴BD
б) Определить   угол между плоскостями DНC и BAC .
В   ΔHDC   проведем HE ┴ CD   ( E∈ [CD] )   и E соединим с вершиной B.
<BEH будет искомый угол ;
tq(<BEH) =BH/BE = b :(b*√3)/2 =2/√3 ; [Δ BEC :   B E =BC*sin60°=b*√3/2 ] .

<BEH = arctq(2/√3).

4,7(50 оценок)

Это интересно:

Здоровье

27.09.2022

5 простых советов по уходу за зубными протезами...

17.12.2021

Секреты экономии денег для студентов...

Компьютеры-и-электроника

12.10.2021

Как присоединить разъем коаксиального кабеля...

Компьютеры-и-электроника

13.03.2023