В правильном тетраэдре ABCD с ребром 2 точка М — середина ВD.
а) Докажите, что прямая ВD перпендикулярна плоскости АМС.
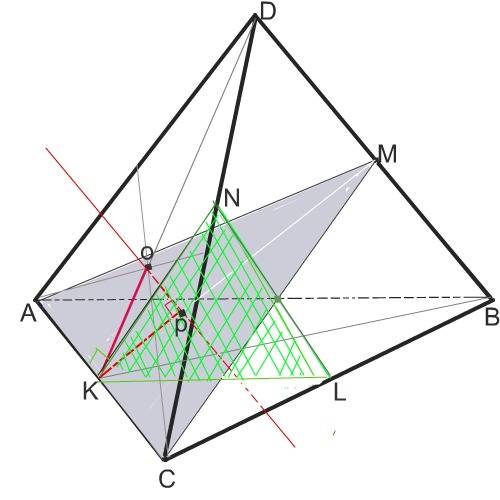
Если соединить середину АС с вершинами тетраэдра D и В, то получим равнобедренный треугольникDКВ со сторонами - апофемами граней АDС и АВС, в котором высота КМ этого треугольника перпендикулярна прямой ВD.
А как известно:
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
б) Через точку пересечения медиан треугольника АDС проведите прямую, перпендикулярную плоскости АМС.
в) Найдите длину отрезка проведенной прямой, расположенного внутри тетраэдра.
Эту длину найдте по теореме Пифагора из треугольника КОР, образованного отрезками медиан треугольников АМС и АDС, равными по 1/3 этих медиан
( медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины). В этом треугольнике отрезок ОР =1/3 медианы КD и является гипотенузой, отрезок КР медианы КМ треугольника АМС - бóльшим катетом, а искомый отрезок ОР- меньшим катетом.
Замечу, что медиана грани АСD и медана сечения АМС не равны между собой, т.к. эти грани имеют общее основание АС, но разную длину. т.к. КМ меньше К.
г) В каком отношении делит этот отрезок плоскость АМС?
Этот отрезок пересекает эту плоскость в точке пересечения медиан и потому никак ее не делит. (Медиана же любого треугольника делит его на два равновеликих треугольника).
д) Найдите площадь сечения тетраэдра плоскостью, проходящей через середину СМ перпендикулярно прямой АС.
Это сечение параллельно перпендикулярному к прямой АС сечению через апофемы граней ADC и CDB и подобно ему.
Апофема DL по формуле высоты правильного треугольника а √3:2=2√3:2= √3
Так как половина СМ равна половине апофемы ( медианы), то она равна ½ √3
Остальная часть om стороны плоскости сечения равна половине do как противолежащая углу 30 °в и равна 1/4 √3
dm=1/4*√3+2/4*√3=3/4 ·√3 ( 3/4 DL)
Коэффициент подобия сечения через середину СМ и сечения через апофемы равен 3/4
Площадь сечения через апофемы равна площади равнобедренного треугольника, боковые стороны которого равны апофеме, а основание - половине ребра пирамиды как средняя линия.
Высоту этого треугольника найдем по теореме Пифагора
h=√( 3-1)= √2
Площадь сечения KDL равна 1*√2=√2 см²
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Искомая площадь сечения через середину СМ=(9 √2):16 см² ≈ 0,8 см²
-------------------------------
Один из рисунков - где сечение = равносторонний треугольник- неверный, не получается удалить.
∠1=∠2=180-135=45, а∠3=180-2*45=180-90=90
если внешний угол прилежит к ∠3 то ∠3=180-135=45, а∠1=∠2=(180-45)/2=67,5